Menu Close

find-the-value-of-0-t-3-1-e-t-dt-

Tinku Tara 0 Comments
Pin




Question Number 45045 by maxmathsup by imad last updated on 07/Oct/18
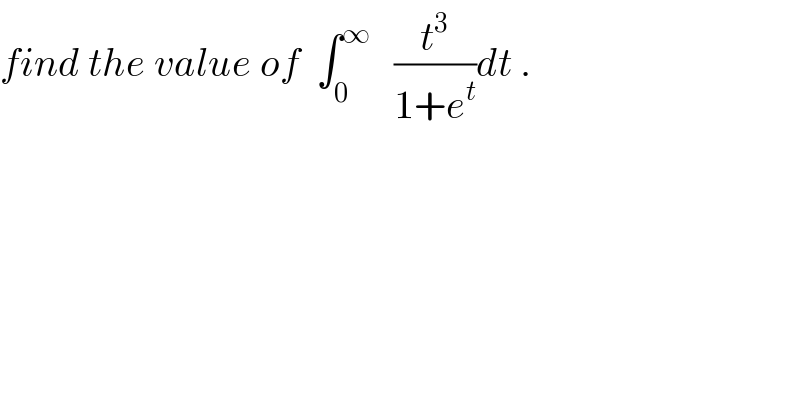
find the value of ∫_0 ^∞ (t^3 /(1+e^t ))dt .
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\mathrm{3}} }{\mathrm{1}+{e}^{{t}} }{dt}\:. \\ $$
Answered by maxmathsup by imad last updated on 09/Oct/18
let A =∫_0 ^∞ (t^3 /(1+e^t )) dt we have A =∫_0 ^∞ ((t^3 e^(−t) )/(1+e^(−t) ))dt =∫_0 ^∞ t^3 e^(−t) (Σ_(n=0) ^∞ (−1)^n e^(−nt) )dt=Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ t^3 e^(−(n+1)t) dt changement (n+1)t =x give A =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ ((x/(n+1)))^3 e^(−x) (dx/((n+1))) =Σ_(n=0) ^∞ (((−1)^n )/((n+1)^4 )) ∫_0 ^∞ x^3 e^(−x) dt let remember that Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt (x>0) ⇒ ∫_0 ^∞ x^3 e^(−x) dx =∫_0 ^∞ x^(4−1) e^(−x) dx =Γ(4) =(4−1)!=3! =6 ⇒ A =6 Σ_(n=0) ^∞ (((−1)^n )/((n+1)^4 )) =6 δ(4) with δ(x)=Σ_(n=1) ^∞ (((−1)^(n−1) )/n^x ) (x>0) let find δ(x) interms of ξ(x)=Σ_(n=1) ^∞ (1/n^x ) we have δ(x)=−Σ_(n=1) ^∞ (1/((2n)^x )) +Σ_(n=0) ^∞ (1/((2n+1)^x )) =−2^(−x) ξ(x) +Σ_(n=0) ^∞ (1/((2n+1)^x )) but ξ(x)=Σ_(n=1) ^∞ (1/((2n)^x )) +Σ_(n=0) ^∞ (1/((2n+1)^x )) =2^(−x) ξ(x)+Σ_(n=0) ^∞ (1/((2n+1)^x )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^x )) =(1−2^(−x) )ξ(x) ⇒ δ(x) =−2^(−x) ξ(x) +(1−2^(−x) )ξ(x) =(1−2^(1−x) )ξ(x) ⇒ δ(4) =(1−2^(−3) )ξ(4) =(1−(1/8))(π^4 /(90)) =(7/8) (π^4 /(90)) ⇒A =6.(7/8) .(π^4 /(90)) ⇒ =((2.3.7)/(2.4)) .(π^4 /(3.30)) = ((7π^4 )/(120))⇒∫_0 ^∞ (t^3 /(1+e^t )) dt =((7 π^4 )/(120)) ★
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{3}} }{\mathrm{1}+{e}^{{t}} }\:{dt}\:\:{we}\:{have}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{3}} {e}^{−{t}} }{\mathrm{1}+{e}^{−{t}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{t}^{\mathrm{3}} {e}^{−{t}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {e}^{−{nt}} \right){dt}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{\mathrm{3}} \:{e}^{−\left({n}+\mathrm{1}\right){t}} {dt} \\ $$$${changement}\:\left({n}+\mathrm{1}\right){t}\:={x}\:{give}\: \\ $$$${A}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \left(\frac{{x}}{{n}+\mathrm{1}}\right)^{\mathrm{3}} {e}^{−{x}} \:\:\frac{{dx}}{\left({n}+\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{4}} }\:\int_{\mathrm{0}} ^{\infty} \:\:{x}^{\mathrm{3}} \:{e}^{−{x}} {dt}\:\:{let}\:{remember}\:{that}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:\left({x}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{x}^{\mathrm{3}} \:{e}^{−{x}} \:{dx}\:=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{4}−\mathrm{1}} {e}^{−{x}} {dx}\:=\Gamma\left(\mathrm{4}\right)\:=\left(\mathrm{4}−\mathrm{1}\right)!=\mathrm{3}!\:=\mathrm{6}\:\Rightarrow \\ $$$${A}\:=\mathrm{6}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{4}} }\:=\mathrm{6}\:\delta\left(\mathrm{4}\right)\:{with}\:\delta\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{{x}} }\:\:\:\left({x}>\mathrm{0}\right)\:{let}\:{find}\:\delta\left({x}\right) \\ $$$${interms}\:{of}\:\xi\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{{x}} }\:\:{we}\:{have}\:\delta\left({x}\right)=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{{x}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} } \\ $$$$=−\mathrm{2}^{−{x}} \:\xi\left({x}\right)\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:{but}\:\xi\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{{x}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} } \\ $$$$=\mathrm{2}^{−{x}} \xi\left({x}\right)+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:=\left(\mathrm{1}−\mathrm{2}^{−{x}} \right)\xi\left({x}\right)\:\Rightarrow \\ $$$$\delta\left({x}\right)\:=−\mathrm{2}^{−{x}} \xi\left({x}\right)\:+\left(\mathrm{1}−\mathrm{2}^{−{x}} \right)\xi\left({x}\right)\:=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{x}} \right)\xi\left({x}\right)\:\Rightarrow \\ $$$$\delta\left(\mathrm{4}\right)\:=\left(\mathrm{1}−\mathrm{2}^{−\mathrm{3}} \right)\xi\left(\mathrm{4}\right)\:=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:=\frac{\mathrm{7}}{\mathrm{8}}\:\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\Rightarrow{A}\:=\mathrm{6}.\frac{\mathrm{7}}{\mathrm{8}}\:.\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\Rightarrow \\ $$$$=\frac{\mathrm{2}.\mathrm{3}.\mathrm{7}}{\mathrm{2}.\mathrm{4}}\:.\frac{\pi^{\mathrm{4}} }{\mathrm{3}.\mathrm{30}}\:=\:\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{120}}\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{3}} }{\mathrm{1}+{e}^{{t}} }\:{dt}\:=\frac{\mathrm{7}\:\pi^{\mathrm{4}} }{\mathrm{120}}\:\bigstar \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *