Question Number 27481 by abdo imad last updated on 07/Jan/18
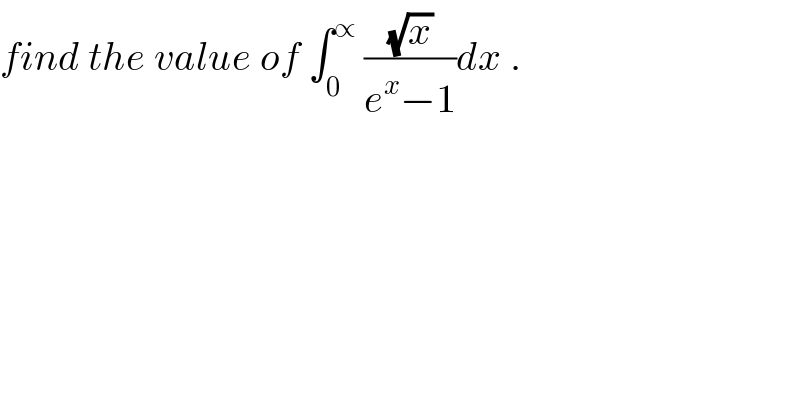
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\propto} \:\frac{\sqrt{{x}}}{{e}^{{x}} −\mathrm{1}}{dx}\:. \\ $$
Commented by abdo imad last updated on 10/Jan/18
![we have proved that ∫_0 ^∞ (t^(x−1) /(e^t −1))=ξ(x)Γ(x) so ∫_0 ^∞ ((√t)/(e^t −1)) dt= ∫_0 ^∞ (t^((3/2)−1) /(e^t −1)) = ξ((3/2)) Γ((3/2)) the relation Γ(x+1)=xΓ(x) give Γ((3/2))=(1/2) Γ((1/2)) but Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒Γ((1/2))= ∫_0 ^∞ (e^(−t) /( (√t)))dt the ch.(√t) =u give ∫_0 ^∞ (e^(−t) /( (√t)))dt==∫_0 ^∞ (e^(−u^2 ) /u)(2u)du= 2∫_0 ^∞ e^(−u^2 ) du = (√π) ⇒ Γ( (1/2))= (√π) ⇒ ∫_0 ^∞ ((√t)/( e^t −1))= (√π) ξ((3/2)) and ξ((3/2))= Σ_(n=1) ^∝ (1/(n(√n))). S_n = Σ_(k=1) ^(n ) (1/(k(√k))) = Σ_(k=1) ^n ∫_k ^(k+1) (dt/(k(√k))) but k≤t≤k+1⇒ (√k)≤(√t)≤(√(k+1))⇒ k(√k) ≤ t(√t)≤(k+1)(√(k+1)) ⇒ (1/((k+1)(√(k+1)))) ≤ (1/(t(√t))) ≤ (1/(k(√k))) ⇒ Σ_(k=1) ^n _( (1/(k+1)(√(k+1))))≤ Σ_(k=1) ^n ∫_k ^(k+1 ) t^(−(3/2)) dt ≤ S_n ⇒ Σ_(k=2) ^(n+1) (1/(k(√k))) ≤ Σ_(k=1) ^n [ (1/(−(3/2)+1))t^(−(3/2)+1) ]_k ^(k+1) ≤ S_n S_n +(1/(n+1)) −1 ≤ −2 Σ_(k=1) ^n ( (k+1)^(−(1/2)) −k^(−(1/2)) )≤ S_n S_n −(n/(n+1)) ≤ −2 Σ_(k=1) ^n ( (1/( (√(k+1)))) − (1/( (√k)))) ≤ S_n S_n −(n/(n+1)) ≤−2( (1/( (√2))) −1 +(1/( (√3) )) − (1/( (√2))) +...(1/( (√(n+1)))) −(1/( (√n)))) ≤ S_n S_(n ) − (n/(n+1)) ≤ −2( (1/( (√(n+1)))) −1) ≤ S_n S_n − (n/(n+1)) ≤ 2− (2/( (√(n+1)))) ≤ S_n .....](https://www.tinkutara.com/question/Q27585.png)
$${we}\:{have}\:{proved}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{x}−\mathrm{1}} }{{e}^{{t}} \:−\mathrm{1}}=\xi\left({x}\right)\Gamma\left({x}\right) \\ $$$${so}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{{t}}}{{e}^{{t}} \:−\mathrm{1}}\:{dt}=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} }{{e}^{{t}} \:−\mathrm{1}}\:=\:\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$${the}\:{relation}\:\Gamma\left({x}+\mathrm{1}\right)={x}\Gamma\left({x}\right)\:{give}\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${but}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:\Rightarrow\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{t}} }{\:\sqrt{{t}}}{dt}\:\:{the}\:{ch}.\sqrt{{t}}\:={u} \\ $$$$ \\ $$$${give}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{t}} }{\:\sqrt{{t}}}{dt}==\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{u}^{\mathrm{2}} } }{{u}}\left(\mathrm{2}{u}\right){du}=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } {du}\:=\:\sqrt{\pi} \\ $$$$\Rightarrow\:\Gamma\left(\:\frac{\mathrm{1}}{\mathrm{2}}\right)=\:\sqrt{\pi} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{{t}}}{\:{e}^{{t}} \:−\mathrm{1}}=\:\sqrt{\pi}\:\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:\:\:\:{and}\:\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\frac{\mathrm{1}}{{n}\sqrt{{n}}}. \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}\:} \:\:\frac{\mathrm{1}}{{k}\sqrt{{k}}}\:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{dt}}{{k}\sqrt{{k}}} \\ $$$${but}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}\leqslant{t}\leqslant{k}+\mathrm{1}\Rightarrow\:\sqrt{{k}}\leqslant\sqrt{{t}}\leqslant\sqrt{{k}+\mathrm{1}}\Rightarrow\:\:\:{k}\sqrt{{k}}\:\:\:\leqslant\:\:\:{t}\sqrt{{t}}\leqslant\left({k}+\mathrm{1}\right)\sqrt{{k}+\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\:\:\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\sqrt{{k}+\mathrm{1}}}\:\:\:\:\:\:\:\:\leqslant\:\:\:\frac{\mathrm{1}}{{t}\sqrt{{t}}}\:\:\:\:\:\:\leqslant\:\:\frac{\mathrm{1}}{{k}\sqrt{{k}}} \\ $$$$\Rightarrow\:\:\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:_{\left(\right.} \frac{\mathrm{1}}{\left.{k}+\mathrm{1}\right)\sqrt{{k}+\mathrm{1}}}\leqslant\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \int_{{k}} ^{{k}+\mathrm{1}\:} {t}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\:{dt}\:\leqslant\:\:{S}_{{n}} \\ $$$$\Rightarrow\:\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\:\frac{\mathrm{1}}{{k}\sqrt{{k}}}\:\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\left[\:\:\frac{\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}}{t}^{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}} \right]_{{k}} ^{{k}+\mathrm{1}} \:\:\leqslant\:{S}_{{n}} \\ $$$${S}_{{n}} \:\:\:+\frac{\mathrm{1}}{{n}+\mathrm{1}}\:−\mathrm{1}\:\:\leqslant\:−\mathrm{2}\:\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \left(\:\left({k}+\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:−{k}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)\leqslant\:{S}_{{n}} \\ $$$${S}_{{n}} \:\:−\frac{{n}}{{n}+\mathrm{1}}\:\:\leqslant\:\:−\mathrm{2}\:\sum_{{k}=\mathrm{1}} ^{{n}} \left(\:\:\frac{\mathrm{1}}{\:\sqrt{{k}+\mathrm{1}}}\:\:−\:\frac{\mathrm{1}}{\:\sqrt{{k}}}\right)\:\:\leqslant\:{S}_{{n}} \\ $$$${S}_{{n}} \:−\frac{{n}}{{n}+\mathrm{1}}\:\:\leqslant−\mathrm{2}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\mathrm{1}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}\:−\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+…\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}\:−\frac{\mathrm{1}}{\:\sqrt{{n}}}\right)\:\leqslant\:{S}_{{n}} \\ $$$${S}_{{n}\:} \:−\:\frac{{n}}{{n}+\mathrm{1}}\:\leqslant\:−\mathrm{2}\left(\:\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}\:−\mathrm{1}\right)\:\leqslant\:{S}_{{n}} \\ $$$${S}_{{n}} \:\:−\:\frac{{n}}{{n}+\mathrm{1}}\:\leqslant\:\mathrm{2}−\:\frac{\mathrm{2}}{\:\sqrt{{n}+\mathrm{1}}}\:\:\leqslant\:{S}_{{n}} \:\:\:\:….. \\ $$
