Question Number 129019 by bramlexs22 last updated on 12/Jan/21

$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\:\mathrm{3}\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{4}} +\mathrm{6}\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} + \\ $$$$\:\mathrm{4}\left(\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}\right). \\ $$
Answered by MJS_new last updated on 12/Jan/21
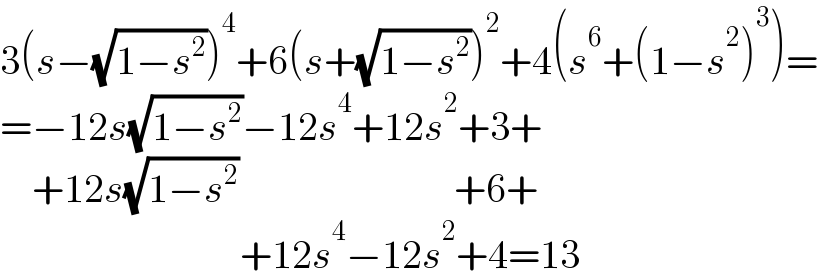
$$\mathrm{3}\left({s}−\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\right)^{\mathrm{4}} +\mathrm{6}\left({s}+\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{4}\left({s}^{\mathrm{6}} +\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{3}} \right)= \\ $$$$=−\mathrm{12}{s}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }−\mathrm{12}{s}^{\mathrm{4}} +\mathrm{12}{s}^{\mathrm{2}} +\mathrm{3}+ \\ $$$$\:\:\:\:+\mathrm{12}{s}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{6}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{12}{s}^{\mathrm{4}} −\mathrm{12}{s}^{\mathrm{2}} +\mathrm{4}=\mathrm{13} \\ $$
Commented by bramlexs22 last updated on 12/Jan/21

$$\mathrm{amazing}\:\mathrm{prof} \\ $$
