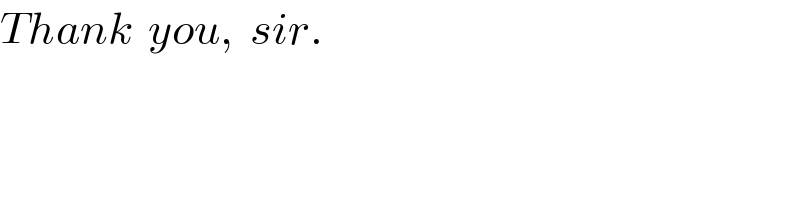Find-the-value-of-a-such-that-2-lt-2x-a-x-2-1-lt-2-

Question Number 160848 by naka3546 last updated on 07/Dec/21

F i n d t h e v a l u e o f a s u c h t h a t

- 2 < \frac{2 x + a}{x^{2} + 1} < 2

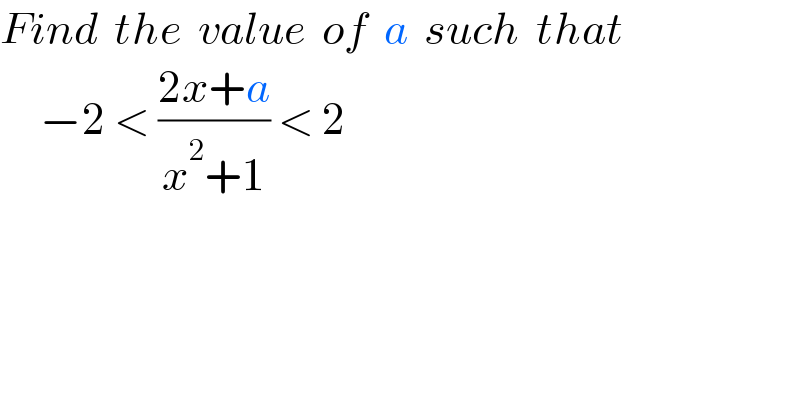
Answered by kowalsky78 last updated on 08/Dec/21

I t h i n k t h e c o r r e c t a n s w e r i s a = - \frac{3}{2} .

Commented by naka3546 last updated on 08/Dec/21

p r o v e i t, p l e a s e .

Answered by mr W last updated on 08/Dec/21

- 2 < \frac{2 x + a}{x^{2} + 1} < 2

- 2 x^{2} - 2 < 2 x + a < 2 x^{2} + 2

(1) :

- 2 x^{2} - 2 < 2 x + a

2 x^{2} + 2 x + a + 2 > 0

2 {(x + \frac{1}{2})}^{2} + a + \frac{3}{2} > 0

a + \frac{3}{2} > 0

\Rightarrow a > - \frac{3}{2}

(2) :

2 x + a < 2 x^{2} + 2

2 x^{2} - 2 x + 2 - a > 0

2 {(x - \frac{1}{2})}^{2} + \frac{3}{2} - a > 0

\frac{3}{2} - a > 0

\Rightarrow a < \frac{3}{2}

(1) + (2) :

- \frac{3}{2} < a < \frac{3}{2}

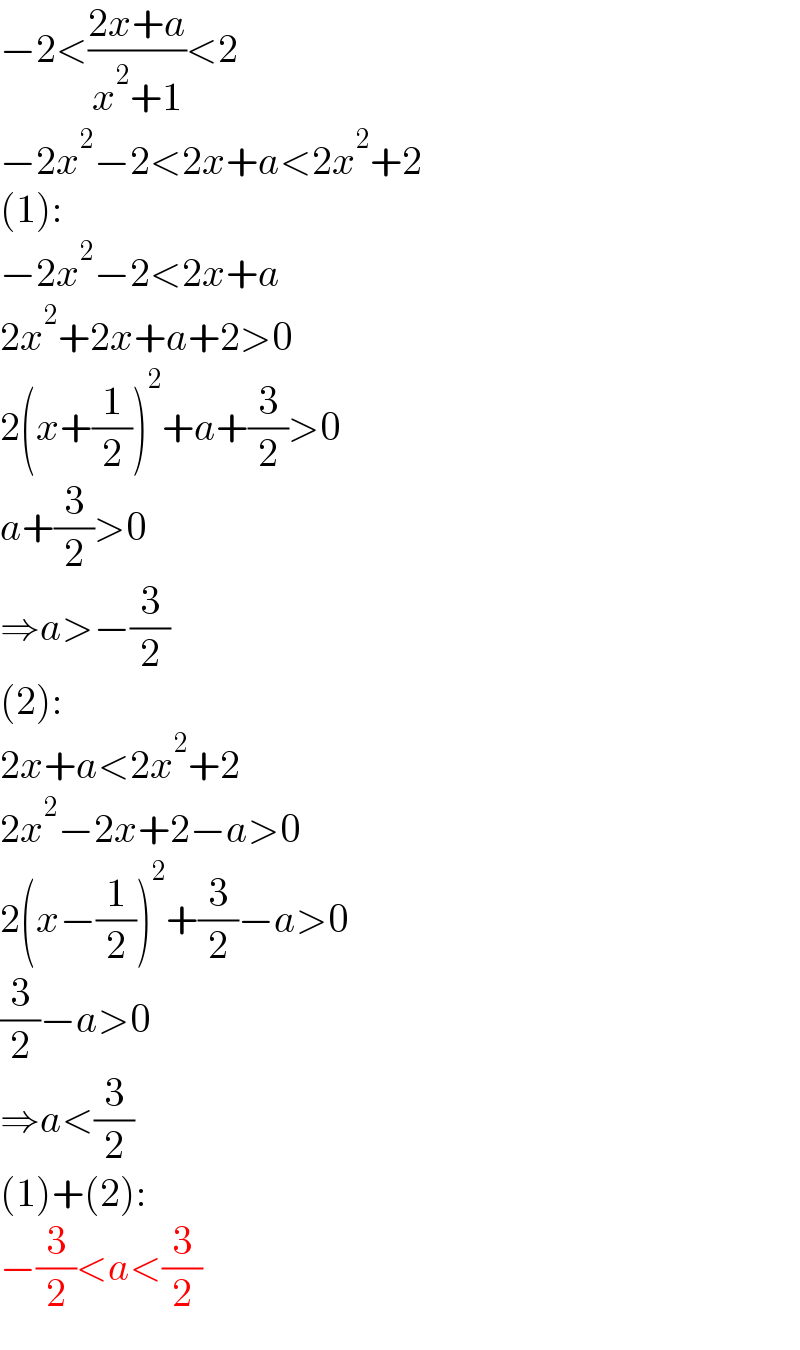
Commented by naka3546 last updated on 08/Dec/21

T h a n k y o u, s i r .