Question Number 35215 by abdo mathsup 649 cc last updated on 16/May/18
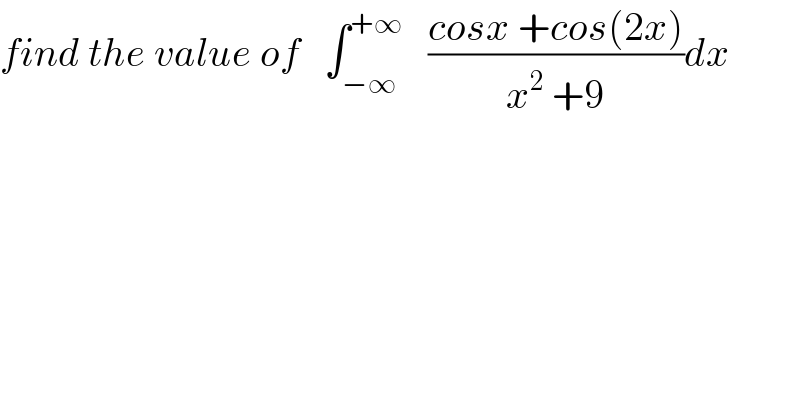
$${find}\:{the}\:{value}\:{of}\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cosx}\:+{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{9}}{dx} \\ $$
Commented by abdo mathsup 649 cc last updated on 23/May/18

$${let}\:{put}\:{I}\:\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{cosx}\:+{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{9}}{dx} \\ $$$$=\:{Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{ix}} \:\:+\:{e}^{{i}\mathrm{2}{x}} }{{x}^{\mathrm{2}} \:+\mathrm{9}}{dx}\right)\:{let}\:{consider}\:{the}\:{complex} \\ $$$${function}\:\varphi\left({z}\right)\:=\:\frac{{e}^{{iz}} \:\:+{e}^{{i}\mathrm{2}{z}} }{{z}^{\mathrm{2}} \:+\mathrm{9}} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{iz}} \:+{e}^{{i}\mathrm{2}{z}} }{\left({z}−\mathrm{3}{i}\right)\left({z}+\mathrm{3}{i}\right)}\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are} \\ $$$$\mathrm{3}{i}\:{and}\:−\mathrm{3}{i}\left({simples}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\mathrm{3}{i}\right) \\ $$$${Res}\left(\varphi,\mathrm{3}{i}\right)\:=\:\frac{{e}^{{i}\left(\mathrm{3}{i}\right)} \:+{e}^{\mathrm{2}{i}\left(\mathrm{3}{i}\right)} }{\mathrm{6}{i}}\:=\:\frac{{e}^{−\mathrm{3}} \:+\:{e}^{−\mathrm{6}} }{\mathrm{6}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{{e}^{−\mathrm{3}} \:+{e}^{−\mathrm{6}} }{\mathrm{6}{i}}\:=\frac{\pi}{\mathrm{3}}\left\{\:{e}^{−\mathrm{3}} \:+{e}^{−\mathrm{6}} \right\}\:\Rightarrow \\ $$$$\bigstar\:\:{I}\:\:=\:\frac{\pi}{\mathrm{3}}\left\{\:{e}^{−\mathrm{3}} \:+{e}^{−\mathrm{6}} \right\}\bigstar \\ $$
