Menu Close

find-the-value-of-cosx-x-2-1-n-dx-n-fromN-and-n-1-

Tinku Tara 0 Comments
Pin




Question Number 163109 by mathmax by abdo last updated on 03/Jan/22
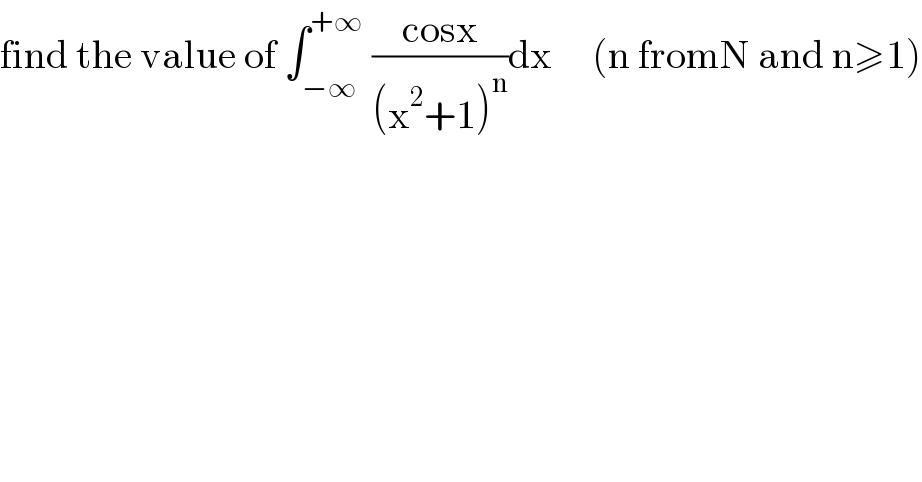
find the value of ∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^n ))dx (n fromN and n≥1)
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx}\:\:\:\:\:\left(\mathrm{n}\:\mathrm{fromN}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 05/Jan/22
A_n =Re(∫_(−∞) ^(+∞) (e^(ix) /((x^2 +1)^n ))dx) let Ψ(z)=(e^(iz) /((z^2 +1)^n )) ⇒ Ψ(z)=(e^(iz) /((z−i)^n (z+i)^n )) the poles of Ψ are i and −i(ordre=n) ∫_R Ψ(z)dz =2iπ Res(Ψ,i) Res(Ψ,i)=lim_(z→i) (1/((n−1)!)){(z−i)^n Ψ(z)}^()n−1)) =(1/((n−1)!))lim_(z→i) {(z+i)^(−n) e^(iz) }^((n−1)) =(1/((n−1)!))lim_(z→i) Σ_(k=0) ^(n−1) C_(n−1) ^k {(z+i)^(−n) }^((k)) (e^(iz) )^((n−1−k)) we have (e^(iz) )^((n−1−k)) =i^(n−1−k) e^(iz) let find (z+i)^p }^((k)) (z+i)^p }^((1)) =p(z+i)^(p−1) (z+i)^p }^((2)) =p(p−1)(z+i)^(p−2) ⇒by recurrence (z+i)^p }^((k)) =p(p−1)....(p−k+1)(z+i)^(p−k) ⇒ {(z+i)^(−n) }^((k)) =(−n)(−n−1)....(−n−k+1)(z+i)^(−n−k) =(−1)^k n(n+1)...(n+k−1)(z+i)^(−n−k) ⇒ Res(Ψ,i)=(1/((n−1)!)) e^(−1) Σ_(k=0) ^(n−1) C_(n−1) ^k i^(n−1−k) (−1)^k n(n+1)...(n+k−1)(2i)^(−n−k) =(1/((n−1)!))e^(−1) Σ_(k=0) ^(n−1) C_(n−1) ^k ((i^(n−1−k) (−1)^k n(n+1)....(n+k−1)i^(−n−k) )/(2^(n+k) )) =(e^(−1) /(2^n (n−1)!))Σ_(k=0) ^(n−1) C_(n−1) ^k (−i)(−1)^(2k) ((n(n+1)....(n+k−1))/2^k ) ⇒ ∫_R Ψ(z)dz =((2πe^(−1) )/(2^n (n−1)!))Σ_(k=0) ^(n−1) ((n(n+1)...(n+k−1))/2^k )×C_n ^k =Re(∫....)=∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^n ))dx
$$\mathrm{A}_{\mathrm{n}} =\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{ix}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx}\right)\:\mathrm{let}\:\Psi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{n}} }\:\Rightarrow \\ $$$$\Psi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{n}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{n}} }\:\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\Psi\:\mathrm{are}\:\mathrm{i}\:\mathrm{and}\:−\mathrm{i}\left(\mathrm{ordre}=\mathrm{n}\right) \\ $$$$\int_{\mathrm{R}} \Psi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\Psi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\Psi,\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{n}} \Psi\left(\mathrm{z}\right)\right\}^{\left.\right)\left.\mathrm{n}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{n}} \:\mathrm{e}^{\mathrm{iz}} \right\}^{\left(\mathrm{n}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\mathrm{C}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{k}} \left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{n}} \right\}^{\left(\mathrm{k}\right)} \:\left(\mathrm{e}^{\mathrm{iz}} \right)^{\left(\mathrm{n}−\mathrm{1}−\mathrm{k}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\left(\mathrm{e}^{\mathrm{iz}} \right)^{\left(\mathrm{n}−\mathrm{1}−\mathrm{k}\right)} =\mathrm{i}^{\mathrm{n}−\mathrm{1}−\mathrm{k}} \:\mathrm{e}^{\mathrm{iz}} \\ $$$$\left.\mathrm{let}\:\mathrm{find}\:\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{k}\right)} \\ $$$$\left.\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{1}\right)} =\mathrm{p}\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}−\mathrm{1}} \:\: \\ $$$$\left.\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{2}\right)} =\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}−\mathrm{2}} \:\Rightarrow\mathrm{by}\:\mathrm{recurrence} \\ $$$$\left.\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{k}\right)} =\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)….\left(\mathrm{p}−\mathrm{k}+\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{p}−\mathrm{k}} \:\Rightarrow \\ $$$$\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{n}} \right\}^{\left(\mathrm{k}\right)} \:=\left(−\mathrm{n}\right)\left(−\mathrm{n}−\mathrm{1}\right)….\left(−\mathrm{n}−\mathrm{k}+\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{n}−\mathrm{k}} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)…\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{n}−\mathrm{k}} \:\Rightarrow \\ $$$$\mathrm{Res}\left(\Psi,\mathrm{i}\right)=\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\:\mathrm{e}^{−\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{C}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{k}} \mathrm{i}^{\mathrm{n}−\mathrm{1}−\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)…\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)\left(\mathrm{2i}\right)^{−\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)!}\mathrm{e}^{−\mathrm{1}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\mathrm{C}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{k}} \:\frac{\mathrm{i}^{\mathrm{n}−\mathrm{1}−\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)….\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)\mathrm{i}^{−\mathrm{n}−\mathrm{k}} }{\mathrm{2}^{\mathrm{n}+\mathrm{k}} \:} \\ $$$$=\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\mathrm{C}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{k}} \:\left(−\mathrm{i}\right)\left(−\mathrm{1}\right)^{\mathrm{2k}} \frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)….\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)}{\mathrm{2}^{\mathrm{k}} }\:\Rightarrow \\ $$$$\int_{\mathrm{R}} \Psi\left(\mathrm{z}\right)\mathrm{dz}\:=\frac{\mathrm{2}\pi\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)…\left(\mathrm{n}+\mathrm{k}−\mathrm{1}\right)}{\mathrm{2}^{\mathrm{k}} }×\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \\ $$$$=\mathrm{Re}\left(\int….\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *