Question Number 39024 by maxmathsup by imad last updated on 01/Jul/18

$${find}\:{the}\:{value}\:{of}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left(\mathrm{2}{x}\right)}{\:\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}\:{dx} \\ $$
Commented by math khazana by abdo last updated on 04/Jul/18
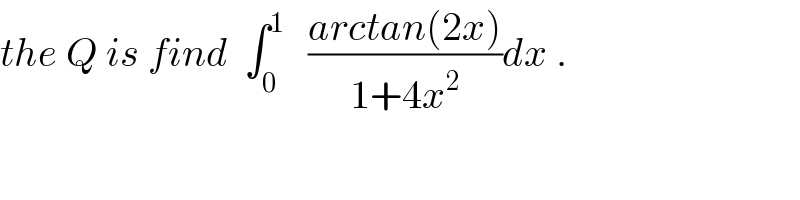
$${the}\:{Q}\:{is}\:{find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 05/Jul/18
![let I = ∫_0 ^1 ((arctan(2x))/(1+4x^2 )) let integrate by parts u^′ =(1/(1+4x^2 )) and v= arctan(2x) ⇒ I =[ (1/2)(arctan(2x))^2 ]_0 ^1 −∫_0 ^1 (1/2)arctan(2x) (2/(1+4x^2 ))dx =(1/2) (arctan(2))^2 −I ⇒ 2I = (1/2){arctan(2)}^2 ⇒I = (1/4){arctan(2)}^2](https://www.tinkutara.com/question/Q39323.png)
$${let}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\:\:{let}\:{integrate}\:{by}\:{parts} \\ $$$${u}^{'} \:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\:\:{and}\:{v}=\:{arctan}\left(\mathrm{2}{x}\right)\:\Rightarrow \\ $$$${I}\:=\left[\:\frac{\mathrm{1}}{\mathrm{2}}\left({arctan}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\mathrm{2}{x}\right)\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left({arctan}\left(\mathrm{2}\right)\right)^{\mathrm{2}} \:\:−{I}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{{arctan}\left(\mathrm{2}\right)\right\}^{\mathrm{2}} \:\Rightarrow{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left\{{arctan}\left(\mathrm{2}\right)\right\}^{\mathrm{2}} \\ $$
