Question Number 30769 by abdo imad last updated on 25/Feb/18
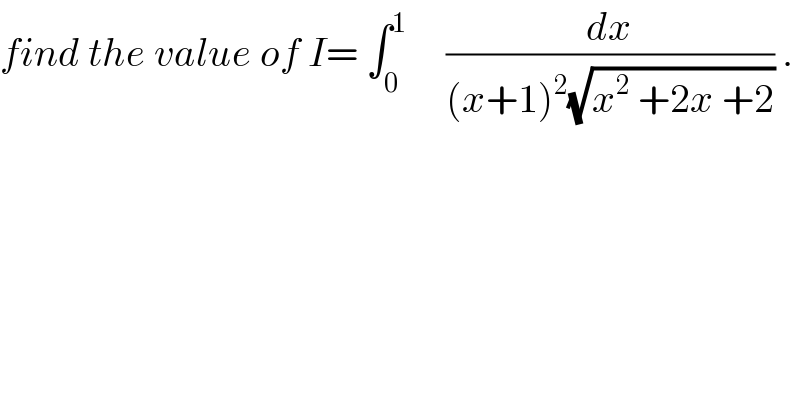
$${find}\:{the}\:{value}\:{of}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{2}}}\:. \\ $$
Commented by abdo imad last updated on 27/Feb/18
![we have x^2 +2x+2=(x+1)^2 +1 the ch=x+1=t give I= ∫_1 ^2 (dt/(t^2 (√(1+t^2 )))) the we can use the ch.t=tanθ ⇒ I= ∫_(π/4) ^(artan2) ((1+tan^2 θ)/(tan^2 θ(√(1+tan^2 θ))))dθ = ∫_(π/4) ^(arctan2) ((cos^2 θ)/(sin^2 θ)) (1/(cosθ))dθ = ∫_(π/4) ^(arctan2) ((cosθ)/(sin^2 θ)) dθ =[−(1/(sinθ))]_(π/4) ^(arctan2) =(√2) − (1/(sin(arctan2))) but we have the formula sin(arctanx)= (x/( (√(1+x^2 ))))( for proof put x=tanθ)⇒ sin(arctan2)= (2/( (√5))) ⇒ I=(√2) −(2/( (√5))) .](https://www.tinkutara.com/question/Q30884.png)
$${we}\:{have}\:{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{2}=\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}\:{the}\:{ch}={x}+\mathrm{1}={t}\:{give} \\ $$$${I}=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:{the}\:{we}\:{can}\:{use}\:{the}\:{ch}.{t}={tan}\theta\:\Rightarrow \\ $$$${I}=\:\int_{\frac{\pi}{\mathrm{4}}} ^{{artan}\mathrm{2}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{{tan}^{\mathrm{2}} \theta\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{d}\theta\:=\:\int_{\frac{\pi}{\mathrm{4}}} ^{{arctan}\mathrm{2}} \:\:\:\frac{{cos}^{\mathrm{2}} \theta}{{sin}^{\mathrm{2}} \theta}\:\frac{\mathrm{1}}{{cos}\theta}{d}\theta \\ $$$$=\:\int_{\frac{\pi}{\mathrm{4}}} ^{{arctan}\mathrm{2}} \:\:\:\:\frac{{cos}\theta}{{sin}^{\mathrm{2}} \theta}\:{d}\theta\:\:=\left[−\frac{\mathrm{1}}{{sin}\theta}\right]_{\frac{\pi}{\mathrm{4}}} ^{{arctan}\mathrm{2}} \\ $$$$=\sqrt{\mathrm{2}}\:−\:\frac{\mathrm{1}}{{sin}\left({arctan}\mathrm{2}\right)}\:{but}\:{we}\:{have}\:{the}\:{formula} \\ $$$${sin}\left({arctanx}\right)=\:\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\left(\:{for}\:{proof}\:{put}\:{x}={tan}\theta\right)\Rightarrow \\ $$$${sin}\left({arctan}\mathrm{2}\right)=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\:\Rightarrow\:{I}=\sqrt{\mathrm{2}}\:\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:. \\ $$
