Question Number 35228 by abdo mathsup 649 cc last updated on 16/May/18
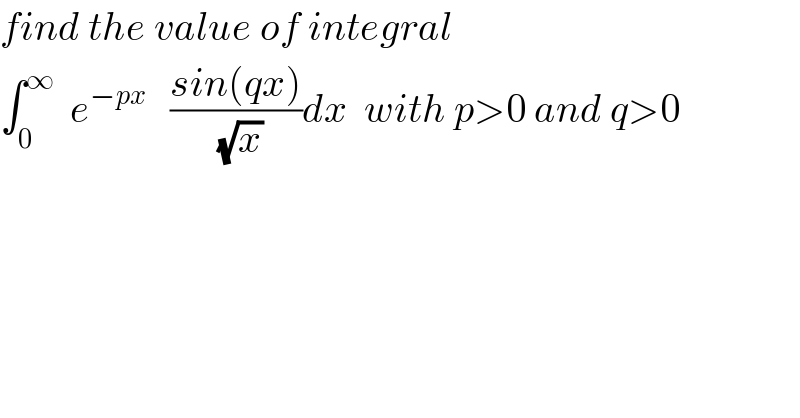
$${find}\:{the}\:{value}\:{of}\:{integral} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{px}} \:\:\:\frac{{sin}\left({qx}\right)}{\:\sqrt{{x}}}{dx}\:\:{with}\:{p}>\mathrm{0}\:{and}\:{q}>\mathrm{0} \\ $$
Commented by abdo mathsup 649 cc last updated on 18/May/18
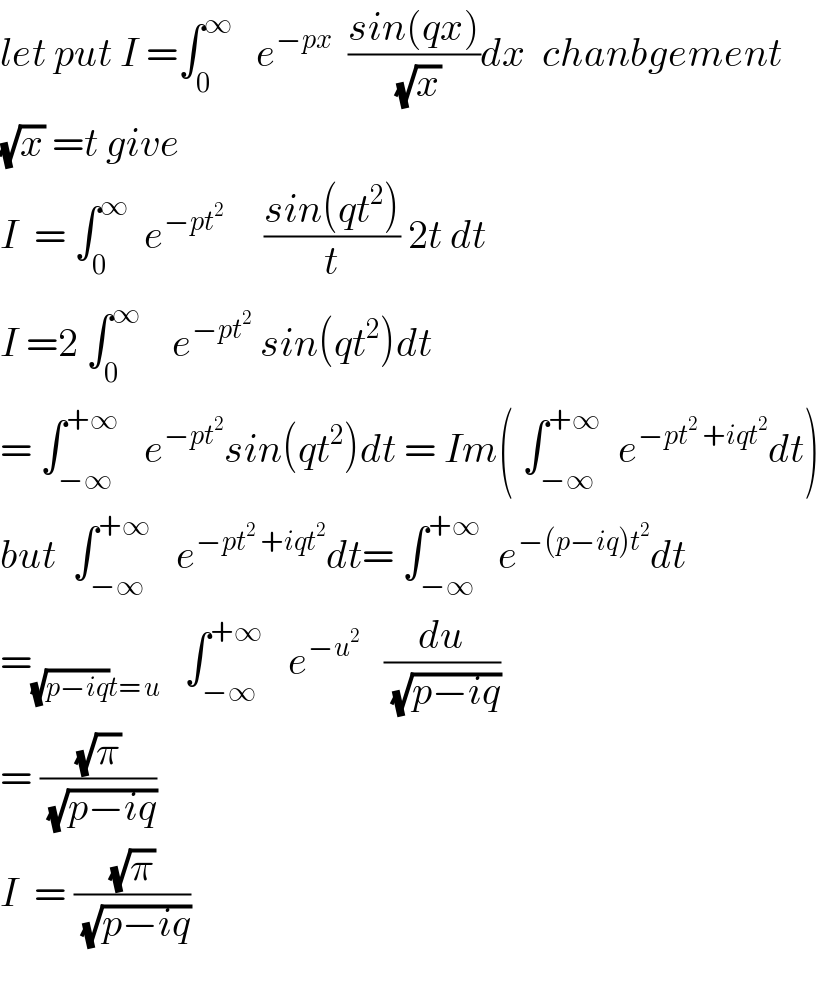
$${let}\:{put}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−{px}} \:\:\frac{{sin}\left({qx}\right)}{\:\sqrt{{x}}}{dx}\:\:{chanbgement} \\ $$$$\sqrt{{x}}\:={t}\:{give} \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{pt}^{\mathrm{2}} } \:\:\:\:\:\frac{{sin}\left({qt}^{\mathrm{2}} \right)}{{t}}\:\mathrm{2}{t}\:{dt} \\ $$$${I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−{pt}^{\mathrm{2}} } \:{sin}\left({qt}^{\mathrm{2}} \right){dt} \\ $$$$=\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−{pt}^{\mathrm{2}} } {sin}\left({qt}^{\mathrm{2}} \right){dt}\:=\:{Im}\left(\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{pt}^{\mathrm{2}} \:+{iqt}^{\mathrm{2}} } {dt}\right) \\ $$$${but}\:\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−{pt}^{\mathrm{2}} \:+{iqt}^{\mathrm{2}} } {dt}=\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({p}−{iq}\right){t}^{\mathrm{2}} } {dt} \\ $$$$=_{\sqrt{{p}−{iq}}{t}=\:{u}} \:\:\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{−{u}^{\mathrm{2}} } \:\:\:\frac{{du}}{\:\sqrt{{p}−{iq}}} \\ $$$$=\:\frac{\sqrt{\pi}}{\:\sqrt{{p}−{iq}}} \\ $$$${I}\:\:=\:\frac{\sqrt{\pi}}{\:\sqrt{{p}−{iq}}} \\ $$$$ \\ $$
Commented by abdo mathsup 649 cc last updated on 18/May/18
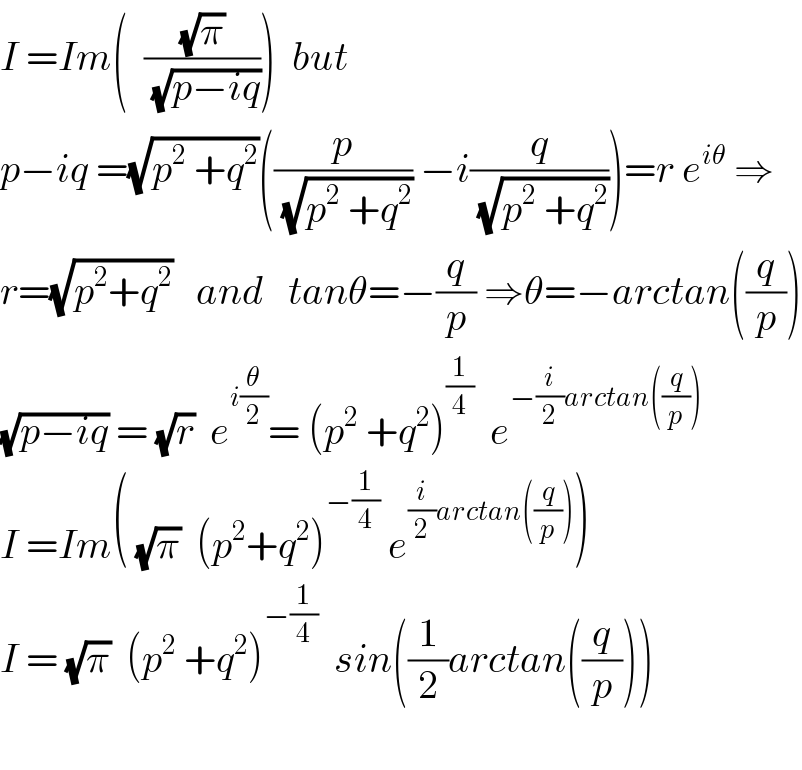
$${I}\:={Im}\left(\:\:\frac{\sqrt{\pi}}{\:\sqrt{{p}−{iq}}}\right)\:\:{but} \\ $$$${p}−{iq}\:=\sqrt{{p}^{\mathrm{2}} \:+{q}^{\mathrm{2}} }\left(\frac{{p}}{\:\sqrt{{p}^{\mathrm{2}} \:+{q}^{\mathrm{2}} }}\:−{i}\frac{{q}}{\:\sqrt{{p}^{\mathrm{2}} \:+{q}^{\mathrm{2}} }}\right)={r}\:{e}^{{i}\theta} \:\Rightarrow \\ $$$${r}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\:\:\:{and}\:\:\:{tan}\theta=−\frac{{q}}{{p}}\:\Rightarrow\theta=−{arctan}\left(\frac{{q}}{{p}}\right) \\ $$$$\sqrt{{p}−{iq}}\:=\:\sqrt{{r}}\:\:{e}^{{i}\frac{\theta}{\mathrm{2}}} =\:\left({p}^{\mathrm{2}} \:+{q}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{{q}}{{p}}\right)} \\ $$$${I}\:={Im}\left(\:\sqrt{\pi}\:\:\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{{q}}{{p}}\right)} \right) \\ $$$${I}\:=\:\sqrt{\pi}\:\:\left({p}^{\mathrm{2}} \:+{q}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{q}}{{p}}\right)\right) \\ $$$$ \\ $$
