find-the-value-of-k-such-that-k-x-2-y-2-y-2x-1-y-2x-3-0-is-a-circle-Hence-obtain-the-centre-and-radius-of-the-resulting-circle-

Question Number 33511 by mondodotto@gmail.com last updated on 18/Apr/18

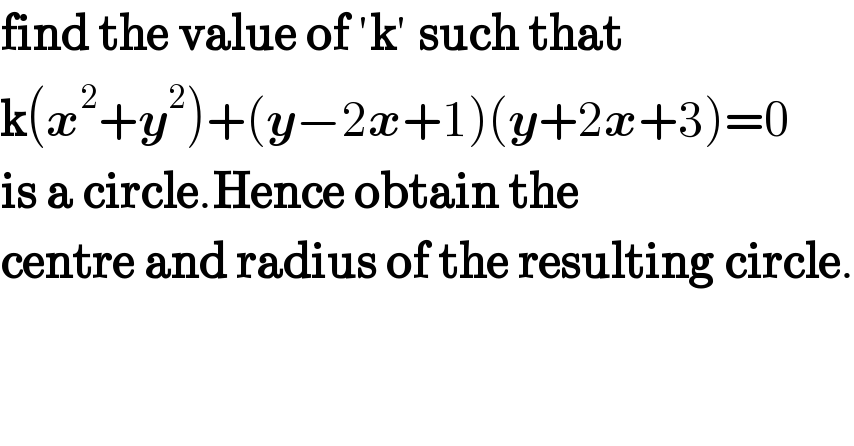
find the value of^{'} k^{'} such that

k (x^{2} + y^{2}) + (y - 2 x + 1) (y + 2 x + 3) = 0

is a circle . Hence obtain the

centre and radius of the resulting circle .

Answered by MJS last updated on 18/Apr/18

(k - 4) x^{2} + (k + 1) y^{2} - 4 x + 4 y + 3 = 0

any circle has the equation

{(x - m)}^{2} + {(y - n)}^{2} - r^{2} = 0

you can multiply this with a

c onstant

c \times {(x - m)}^{2} + c \times {(y - n)}^{2} - c \times r^{2} = 0

but the coefficients of x^{2} and y^{2}

are always identical

k - 4 = k + 1

has no solution \Rightarrow no circle

Commented by mondodotto@gmail.com last updated on 18/Apr/18

thanx a lot god bless you