Question Number 57332 by problem solverd last updated on 02/Apr/19
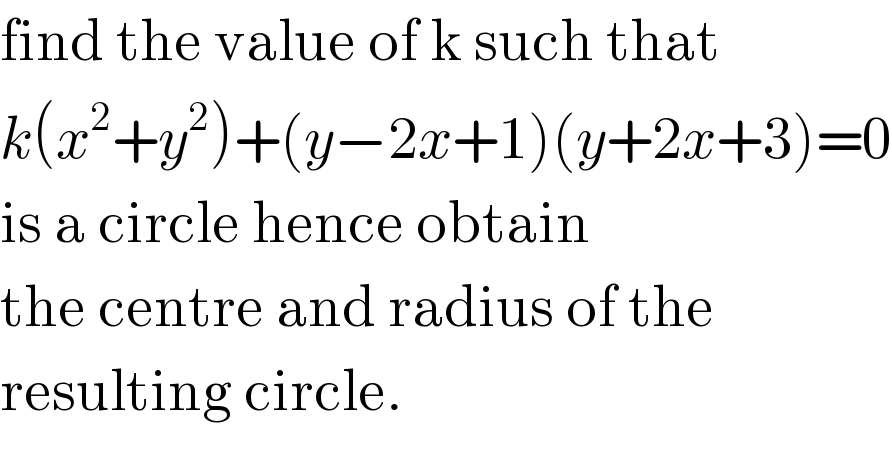
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}\:\mathrm{such}\:\mathrm{that} \\ $$$${k}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\left({y}−\mathrm{2}{x}+\mathrm{1}\right)\left({y}+\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{hence}\:\mathrm{obtain}\: \\ $$$$\mathrm{the}\:\mathrm{centre}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{resulting}\:\mathrm{circle}. \\ $$
Commented by mr W last updated on 03/Apr/19

$${k}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+{y}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} +….=\mathrm{0} \\ $$$$\left({k}−\mathrm{4}\right){x}^{\mathrm{2}} +\left({k}+\mathrm{1}\right){y}^{\mathrm{2}} +….=\mathrm{0} \\ $$$${for}\:{the}\:{equation}\:{of}\:{a}\:{circle}\:{the} \\ $$$${coefficients}\:{of}\:{x}^{\mathrm{2}} \:{and}\:{y}^{\mathrm{2}} \:{must}\:{be}\:{the} \\ $$$${same}. \\ $$$${k}−\mathrm{4}\overset{?} {=}{k}+\mathrm{1}\:\Rightarrow{no}\:{solution}\:{for}\:{k} \\ $$$$\Rightarrow{the}\:{given}\:{equation}\:{can}\:{not}\:{be}\:{a}\:{circle}! \\ $$$$ \\ $$$${please}\:{recheck}\:{the}\:{question}. \\ $$
