Menu Close

Find-the-value-of-lim-n-k-n-2n-1-k-k-

Tinku Tara 0 Comments
Pin




Question Number 144261 by ZiYangLee last updated on 23/Jun/21
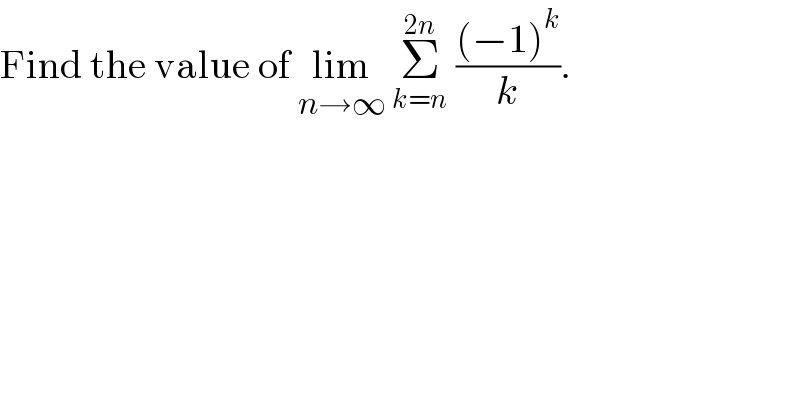
Find the value of lim_(n→∞) Σ_(k=n) ^(2n) (((−1)^k )/k).
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}. \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/21
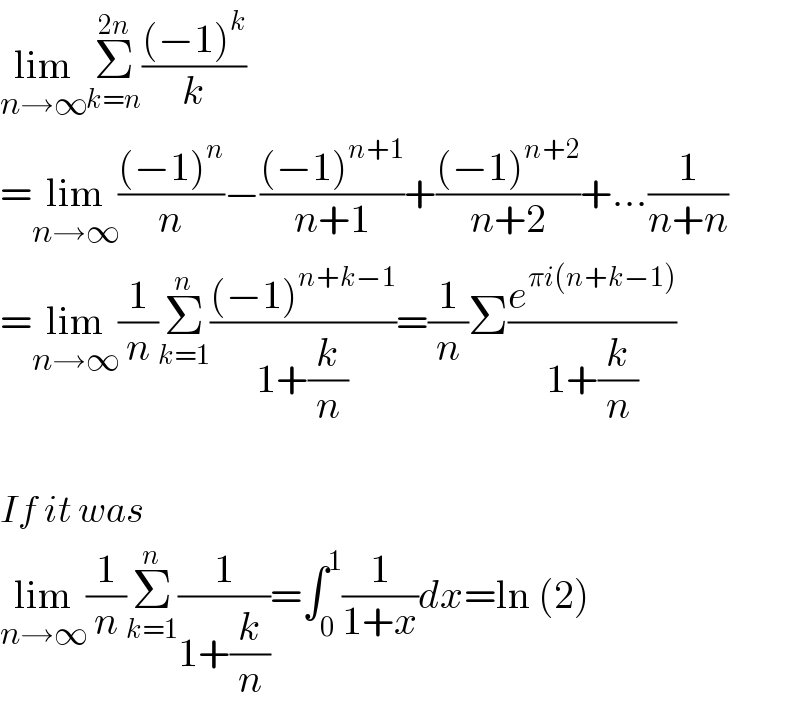
lim_(n→∞) Σ_(k=n) ^(2n) (((−1)^k )/k) =lim_(n→∞) (((−1)^n )/n)−(((−1)^(n+1) )/(n+1))+(((−1)^(n+2) )/(n+2))+...(1/(n+n)) =lim_(n→∞) (1/n)Σ_(k=1) ^n (((−1)^(n+k−1) )/(1+(k/n)))=(1/n)Σ(e^(πi(n+k−1)) /(1+(k/n))) If it was lim_(n→∞) (1/n)Σ_(k=1) ^n (1/(1+(k/n)))=∫_0 ^1 (1/(1+x))dx=ln (2)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}−\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{2}} }{{n}+\mathrm{2}}+…\frac{\mathrm{1}}{{n}+{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}−\mathrm{1}} }{\mathrm{1}+\frac{{k}}{{n}}}=\frac{\mathrm{1}}{{n}}\Sigma\frac{{e}^{\pi{i}\left({n}+{k}−\mathrm{1}\right)} }{\mathrm{1}+\frac{{k}}{{n}}} \\ $$$$ \\ $$$${If}\:{it}\:{was}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$
Answered by mathmax by abdo last updated on 24/Jun/21
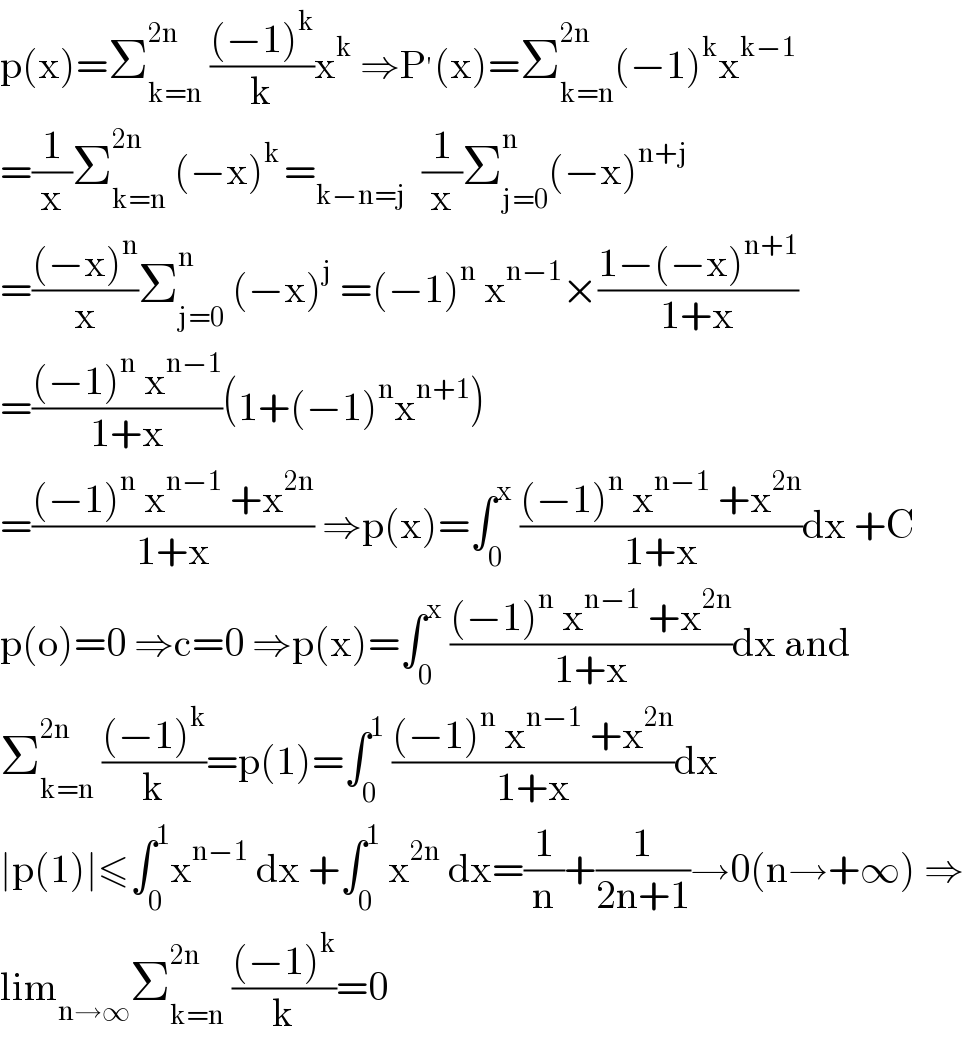
p(x)=Σ_(k=n) ^(2n) (((−1)^k )/k)x^k ⇒P^′ (x)=Σ_(k=n) ^(2n) (−1)^k x^(k−1) =(1/x)Σ_(k=n) ^(2n) (−x)^(k ) =_(k−n=j) (1/x)Σ_(j=0) ^n (−x)^(n+j) =(((−x)^n )/x)Σ_(j=0) ^n (−x)^j =(−1)^n x^(n−1) ×((1−(−x)^(n+1) )/(1+x)) =(((−1)^n x^(n−1) )/(1+x))(1+(−1)^n x^(n+1) ) =(((−1)^n x^(n−1) +x^(2n) )/(1+x)) ⇒p(x)=∫_0 ^x (((−1)^n x^(n−1) +x^(2n) )/(1+x))dx +C p(o)=0 ⇒c=0 ⇒p(x)=∫_0 ^x (((−1)^n x^(n−1) +x^(2n) )/(1+x))dx and Σ_(k=n) ^(2n) (((−1)^k )/k)=p(1)=∫_0 ^1 (((−1)^n x^(n−1) +x^(2n) )/(1+x))dx ∣p(1)∣≤∫_0 ^1 x^(n−1) dx +∫_0 ^1 x^(2n) dx=(1/n)+(1/(2n+1))→0(n→+∞) ⇒ lim_(n→∞) Σ_(k=n) ^(2n) (((−1)^k )/k)=0
$$\mathrm{p}\left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\mathrm{x}^{\mathrm{k}} \:\Rightarrow\mathrm{P}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{k}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}\sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \:\left(−\mathrm{x}\right)^{\mathrm{k}\:} =_{\mathrm{k}−\mathrm{n}=\mathrm{j}} \:\:\frac{\mathrm{1}}{\mathrm{x}}\sum_{\mathrm{j}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{x}\right)^{\mathrm{n}+\mathrm{j}} \\ $$$$=\frac{\left(−\mathrm{x}\right)^{\mathrm{n}} }{\mathrm{x}}\sum_{\mathrm{j}=\mathrm{0}} ^{\mathrm{n}} \:\left(−\mathrm{x}\right)^{\mathrm{j}} \:=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} ×\frac{\mathrm{1}−\left(−\mathrm{x}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{1}+\mathrm{x}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}}\left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} \right) \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}+\mathrm{x}}\:\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{x}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:+\mathrm{C} \\ $$$$\mathrm{p}\left(\mathrm{o}\right)=\mathrm{0}\:\Rightarrow\mathrm{c}=\mathrm{0}\:\Rightarrow\mathrm{p}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{x}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\mathrm{and} \\ $$$$\sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}=\mathrm{p}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\mid\mathrm{p}\left(\mathrm{1}\right)\mid\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\mathrm{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\rightarrow\mathrm{0}\left(\mathrm{n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *