Question Number 31978 by abdo imad last updated on 17/Mar/18
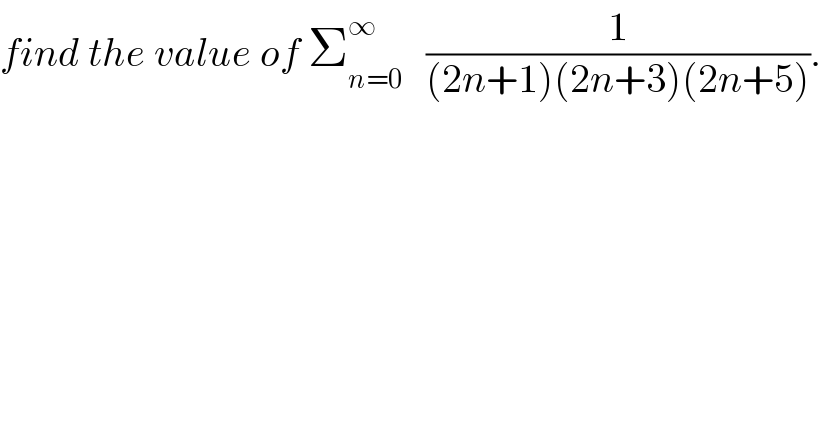
$${find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)\left(\mathrm{2}{n}+\mathrm{5}\right)}. \\ $$
Answered by Joel578 last updated on 18/Mar/18
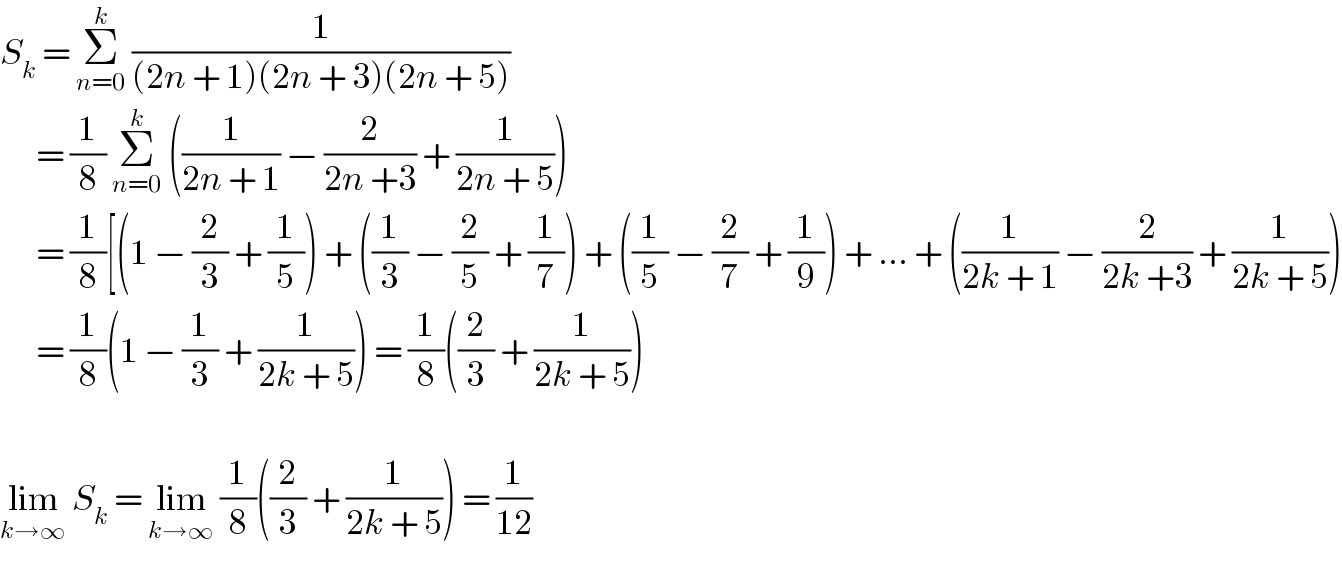
$${S}_{{k}} \:=\:\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)\left(\mathrm{2}{n}\:+\:\mathrm{3}\right)\left(\mathrm{2}{n}\:+\:\mathrm{5}\right)} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{2}{n}\:+\:\mathrm{1}}\:−\:\frac{\mathrm{2}}{\mathrm{2}{n}\:+\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{n}\:+\:\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left[\left(\mathrm{1}\:−\:\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{5}}\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{2}}{\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{7}}\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{5}}\:−\:\frac{\mathrm{2}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{9}}\right)\:+\:…\:+\:\left(\frac{\mathrm{1}}{\mathrm{2}{k}\:+\:\mathrm{1}}\:−\:\frac{\mathrm{2}}{\mathrm{2}{k}\:+\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\:\mathrm{5}}\right)\right. \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\:\mathrm{5}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\:\mathrm{5}}\right) \\ $$$$ \\ $$$$\underset{{k}\rightarrow\infty} {\mathrm{lim}}\:{S}_{{k}} \:=\:\underset{{k}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\:\mathrm{5}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{12}} \\ $$
