Menu Close

find-the-value-of-n-1-1-n-2-n-1-2n-1-

Tinku Tara 0 Comments
Pin




Question Number 33588 by abdo imad last updated on 19/Apr/18
find the value of Σ_(n=1) ^∞ (1/(n^2 (n+1)(2n+1))) .
$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\:. \\ $$
Commented by abdo imad last updated on 20/Apr/18
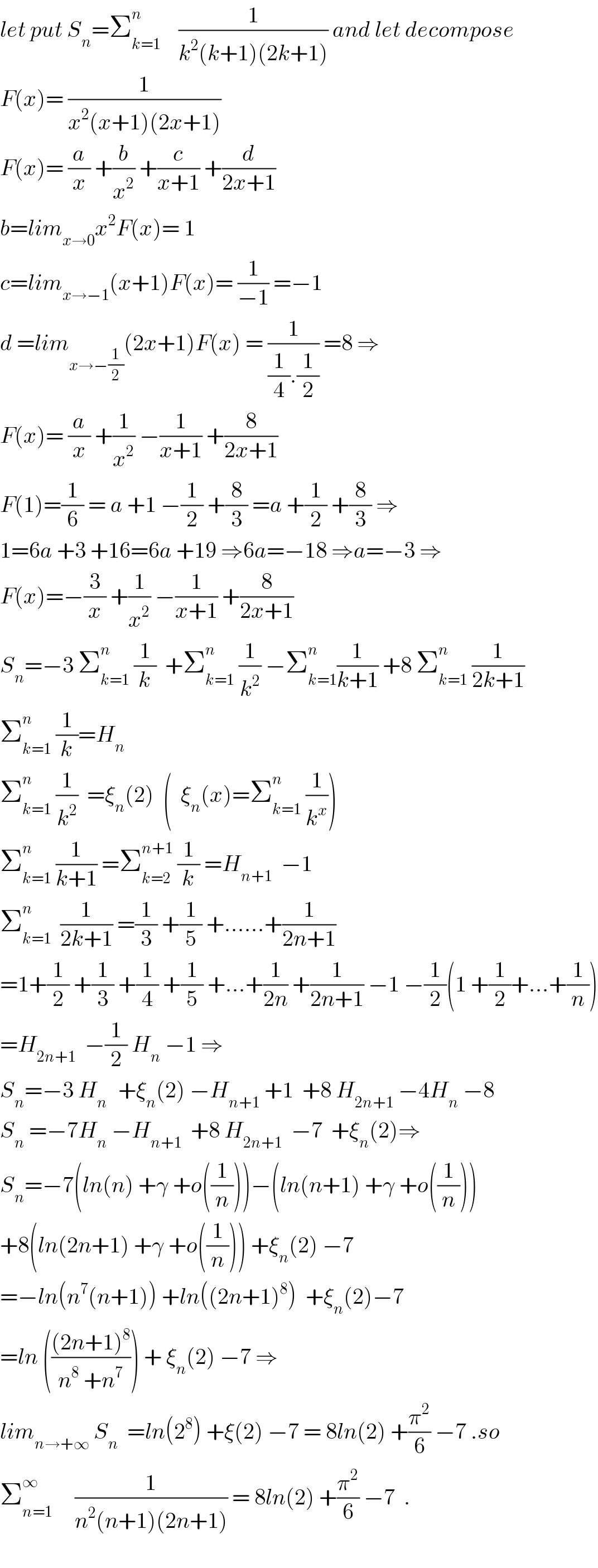
let put S_n =Σ_(k=1) ^n (1/(k^2 (k+1)(2k+1))) and let decompose F(x)= (1/(x^2 (x+1)(2x+1))) F(x)= (a/x) +(b/x^2 ) +(c/(x+1)) +(d/(2x+1)) b=lim_(x→0) x^2 F(x)= 1 c=lim_(x→−1) (x+1)F(x)= (1/(−1)) =−1 d =lim_(x→−(1/2)) (2x+1)F(x) = (1/((1/4).(1/2))) =8 ⇒ F(x)= (a/x) +(1/x^2 ) −(1/(x+1)) +(8/(2x+1)) F(1)=(1/6) = a +1 −(1/2) +(8/3) =a +(1/2) +(8/3) ⇒ 1=6a +3 +16=6a +19 ⇒6a=−18 ⇒a=−3 ⇒ F(x)=−(3/x) +(1/x^2 ) −(1/(x+1)) +(8/(2x+1)) S_n =−3 Σ_(k=1) ^n (1/k) +Σ_(k=1) ^n (1/k^2 ) −Σ_(k=1) ^n (1/(k+1)) +8 Σ_(k=1) ^n (1/(2k+1)) Σ_(k=1) ^n (1/k)=H_n Σ_(k=1) ^n (1/k^2 ) =ξ_n (2) ( ξ_n (x)=Σ_(k=1) ^n (1/k^x )) Σ_(k=1) ^n (1/(k+1)) =Σ_(k=2) ^(n+1) (1/k) =H_(n+1) −1 Σ_(k=1) ^n (1/(2k+1)) =(1/3) +(1/5) +......+(1/(2n+1)) =1+(1/2) +(1/3) +(1/4) +(1/5) +...+(1/(2n)) +(1/(2n+1)) −1 −(1/2)(1 +(1/2)+...+(1/n)) =H_(2n+1) −(1/2) H_n −1 ⇒ S_n =−3 H_(n ) +ξ_n (2) −H_(n+1) +1 +8 H_(2n+1) −4H_n −8 S_n =−7H_n −H_(n+1) +8 H_(2n+1) −7 +ξ_n (2)⇒ S_n =−7(ln(n) +γ +o((1/n)))−(ln(n+1) +γ +o((1/n))) +8(ln(2n+1) +γ +o((1/n))) +ξ_n (2) −7 =−ln(n^7 (n+1)) +ln((2n+1)^8 ) +ξ_n (2)−7 =ln ((((2n+1)^8 )/(n^8 +n^7 ))) + ξ_n (2) −7 ⇒ lim_(n→+∞) S_n =ln(2^8 ) +ξ(2) −7 = 8ln(2) +(π^2 /6) −7 .so Σ_(n=1) ^∞ (1/(n^2 (n+1)(2n+1))) = 8ln(2) +(π^2 /6) −7 .
$${let}\:{put}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\:{and}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{{x}+\mathrm{1}}\:+\frac{{d}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{0}} {x}^{\mathrm{2}} {F}\left({x}\right)=\:\mathrm{1} \\ $$$${c}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{−\mathrm{1}}\:=−\mathrm{1} \\ $$$${d}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{2}{x}+\mathrm{1}\right){F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}}\:=\mathrm{8}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{8}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{6}}\:=\:{a}\:+\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{8}}{\mathrm{3}}\:={a}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{8}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{1}=\mathrm{6}{a}\:+\mathrm{3}\:+\mathrm{16}=\mathrm{6}{a}\:+\mathrm{19}\:\Rightarrow\mathrm{6}{a}=−\mathrm{18}\:\Rightarrow{a}=−\mathrm{3}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{3}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{8}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${S}_{{n}} =−\mathrm{3}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:−\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{k}+\mathrm{1}}\:+\mathrm{8}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}={H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:\:=\xi_{{n}} \left(\mathrm{2}\right)\:\:\left(\:\:\xi_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{{x}} }\right) \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}+\mathrm{1}} \:\:−\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+……+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+…+\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:−\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}+…+\frac{\mathrm{1}}{{n}}\right) \\ $$$$={H}_{\mathrm{2}{n}+\mathrm{1}} \:\:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:−\mathrm{1}\:\Rightarrow \\ $$$${S}_{{n}} =−\mathrm{3}\:{H}_{{n}\:} \:\:+\xi_{{n}} \left(\mathrm{2}\right)\:−{H}_{{n}+\mathrm{1}} \:+\mathrm{1}\:\:+\mathrm{8}\:{H}_{\mathrm{2}{n}+\mathrm{1}} \:−\mathrm{4}{H}_{{n}} \:−\mathrm{8} \\ $$$${S}_{{n}} \:=−\mathrm{7}{H}_{{n}} \:−{H}_{{n}+\mathrm{1}} \:\:+\mathrm{8}\:{H}_{\mathrm{2}{n}+\mathrm{1}} \:\:−\mathrm{7}\:\:+\xi_{{n}} \left(\mathrm{2}\right)\Rightarrow \\ $$$${S}_{{n}} =−\mathrm{7}\left({ln}\left({n}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)−\left({ln}\left({n}+\mathrm{1}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right) \\ $$$$+\mathrm{8}\left({ln}\left(\mathrm{2}{n}+\mathrm{1}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)\:+\xi_{{n}} \left(\mathrm{2}\right)\:−\mathrm{7} \\ $$$$=−{ln}\left({n}^{\mathrm{7}} \left({n}+\mathrm{1}\right)\right)\:+{ln}\left(\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{8}} \right)\:\:+\xi_{{n}} \left(\mathrm{2}\right)−\mathrm{7} \\ $$$$={ln}\:\left(\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{8}} }{{n}^{\mathrm{8}} \:+{n}^{\mathrm{7}} }\right)\:+\:\xi_{{n}} \left(\mathrm{2}\right)\:−\mathrm{7}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:\:={ln}\left(\mathrm{2}^{\mathrm{8}} \right)\:+\xi\left(\mathrm{2}\right)\:−\mathrm{7}\:=\:\mathrm{8}{ln}\left(\mathrm{2}\right)\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{7}\:.{so} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\:=\:\mathrm{8}{ln}\left(\mathrm{2}\right)\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{7}\:\:. \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 19/Apr/18
Σ_(n=1) ^∞ (1/(n^2 (n+1)(2n+1)))=Σ_(n=1) ^∞ ((a/n)+(b/n^2 )+(c/(n+1))+(d/(2n+1))) with a=−3 ; b=1 ; c=−1 ; d=8 so Σ_(n=1) ^∞ (1/(n^2 (n+1)(2n+1)))=Σ_(n=1) ^∞ (((−3)/n)+(1/n^2 )−(1/(n+1))+(8/(2n+1))) let′s calculate A=Σ_(n=1) ^∞ (8/(2n+1)) A=8((1/3)+(1/5)+(1/7)+...)=8[((1/3)+(1/5)+...)+((1/2)+(1/4)+(1/6)+...)−((1/2)+(1/4)+(1/6)+...)] =8[Σ_(n=2) ^∞ (1/n)−(1/2)(1+(1/2)+(1/3)+(1/4)+...)] =8(Σ_(n=2) ^∞ (1/n)−(1/2)Σ_(n=2) ^∞ (1/n)−(1/2))=4Σ_(n=2) ^∞ (1/n)−4 so Σ_(n=1) ^∞ ((8/(2n+1))−(3/n)−(1/(n+1)))=4Σ_(n=2) ^∞ (1/n)−4−3(Σ_(n=2) ^∞ (1/n)+(1/1))−Σ_(n=1) ^∞ (1/(n+1)) let k=n+1 Σ_(n=1) ^∞ ((8/(2n+1))−(3/n)−(1/(n+1)))=Σ_(n=2) ^∞ (1/n)−7−Σ_(k=2) ^∞ (1/k)=−7 we know that ζ(2)=Σ_(n=1) ^∞ (1/n^2 )=(π^2 /6) (ζ (x) is Riemann zeta function) As results Σ_(n=1) ^∞ (1/(n^2 (n+1)(2n+1)))=(π^2 /6)−7
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{a}}{{n}}+\frac{{b}}{{n}^{\mathrm{2}} }+\frac{{c}}{{n}+\mathrm{1}}+\frac{{d}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$${with}\:\:{a}=−\mathrm{3}\:;\:\:{b}=\mathrm{1}\:;\:{c}=−\mathrm{1}\:;\:\:{d}=\mathrm{8} \\ $$$${so}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{−\mathrm{3}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{8}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$${let}'{s}\:{calculate}\:\:{A}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{8}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$${A}=\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}+…\right)=\mathrm{8}\left[\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+…\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+…\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+…\right)\right] \\ $$$$=\mathrm{8}\left[\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…\right)\right] \\ $$$$=\mathrm{8}\left(\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\mathrm{4} \\ $$$${so}\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{8}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\mathrm{4}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\mathrm{4}−\mathrm{3}\left(\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{\mathrm{1}}\right)−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${let}\:\:{k}={n}+\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{8}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\mathrm{7}−\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}=−\mathrm{7} \\ $$$${we}\:\:{know}\:{that}\:\:\zeta\left(\mathrm{2}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:\left(\zeta\:\left({x}\right)\:\:{is}\:{Riemann}\:{zeta}\:{function}\right) \\ $$$${As}\:{results} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{7} \\ $$
Commented by abdo imad last updated on 20/Apr/18
sir sma3l you have commited a error of calculus because the serie is positif but the value (π^2 /6) −7 is negative but nevermind your method is correct...
$${sir}\:{sma}\mathrm{3}{l}\:{you}\:{have}\:{commited}\:{a}\:{error}\:{of}\:{calculus}\:{because} \\ $$$${the}\:{serie}\:{is}\:{positif}\:\:{but}\:{the}\:{value}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{7}\:{is}\:{negative}\:{but} \\ $$$${nevermind}\:{your}\:{method}\:{is}\:{correct}… \\ $$
Commented by sma3l2996 last updated on 20/Apr/18
That what I just saw. There is an error in my work. Can you check my work please?
$${That}\:{what}\:{I}\:{just}\:{saw}.\:{There}\:{is}\:{an}\:{error}\:{in}\:{my}\:{work}. \\ $$$${Can}\:{you}\:{check}\:{my}\:{work}\:{please}? \\ $$$$ \\ $$
Commented by abdo imad last updated on 20/Apr/18
i advise you sir sma3l to use the harmonic sequence H_n took a look in my method....
$${i}\:{advise}\:{you}\:{sir}\:{sma}\mathrm{3}{l}\:{to}\:{use}\:{the}\:{harmonic}\:{sequence}\:{H}_{{n}} \\ $$$${took}\:{a}\:{look}\:{in}\:{my}\:{method}…. \\ $$
Commented by sma3l2996 last updated on 20/Apr/18
Ok thank you
$${Ok}\:{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *