Menu Close

find-the-value-of-p-pls-help-1-3-3-3-5-3-p-3-8128-

Tinku Tara 0 Comments
Pin




Question Number 104706 by Skabetix last updated on 23/Jul/20
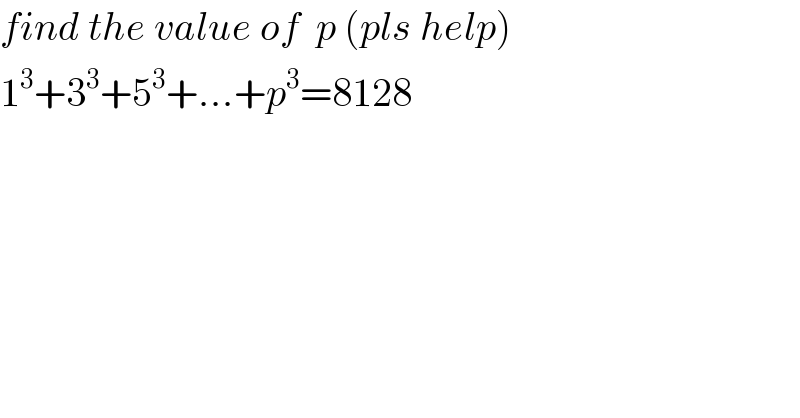
find the value of p (pls help) 1^3 +3^3 +5^3 +...+p^3 =8128
$${find}\:{the}\:{value}\:{of}\:\:{p}\:\left({pls}\:{help}\right) \\ $$$$\mathrm{1}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +\mathrm{5}^{\mathrm{3}} +…+{p}^{\mathrm{3}} =\mathrm{8128} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Jul/20
Commented by mr W last updated on 23/Jul/20
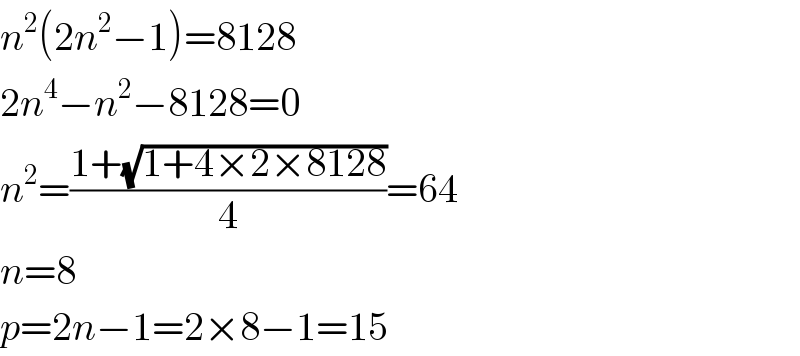
n^2 (2n^2 −1)=8128 2n^4 −n^2 −8128=0 n^2 =((1+(√(1+4×2×8128)))/4)=64 n=8 p=2n−1=2×8−1=15
$${n}^{\mathrm{2}} \left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{8128} \\ $$$$\mathrm{2}{n}^{\mathrm{4}} −{n}^{\mathrm{2}} −\mathrm{8128}=\mathrm{0} \\ $$$${n}^{\mathrm{2}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}×\mathrm{2}×\mathrm{8128}}}{\mathrm{4}}=\mathrm{64} \\ $$$${n}=\mathrm{8} \\ $$$${p}=\mathrm{2}{n}−\mathrm{1}=\mathrm{2}×\mathrm{8}−\mathrm{1}=\mathrm{15} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jul/20
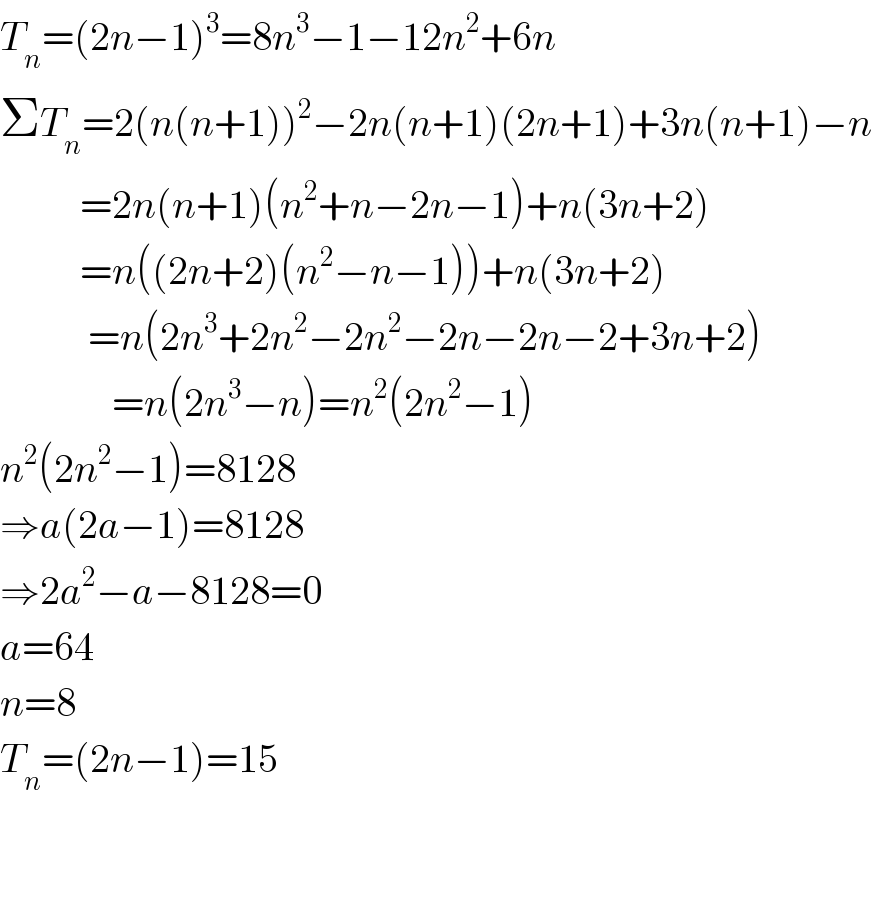
T_n =(2n−1)^3 =8n^3 −1−12n^2 +6n ΣT_n =2(n(n+1))^2 −2n(n+1)(2n+1)+3n(n+1)−n =2n(n+1)(n^2 +n−2n−1)+n(3n+2) =n((2n+2)(n^2 −n−1))+n(3n+2) =n(2n^3 +2n^2 −2n^2 −2n−2n−2+3n+2) =n(2n^3 −n)=n^2 (2n^2 −1) n^2 (2n^2 −1)=8128 ⇒a(2a−1)=8128 ⇒2a^2 −a−8128=0 a=64 n=8 T_n =(2n−1)=15
$${T}_{{n}} =\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{3}} =\mathrm{8}{n}^{\mathrm{3}} −\mathrm{1}−\mathrm{12}{n}^{\mathrm{2}} +\mathrm{6}{n} \\ $$$$\Sigma{T}_{{n}} =\mathrm{2}\left({n}\left({n}+\mathrm{1}\right)\right)^{\mathrm{2}} −\mathrm{2}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)+\mathrm{3}{n}\left({n}+\mathrm{1}\right)−{n} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{n}\left({n}+\mathrm{1}\right)\left({n}^{\mathrm{2}} +{n}−\mathrm{2}{n}−\mathrm{1}\right)+{n}\left(\mathrm{3}{n}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:={n}\left(\left(\mathrm{2}{n}+\mathrm{2}\right)\left({n}^{\mathrm{2}} −{n}−\mathrm{1}\right)\right)+{n}\left(\mathrm{3}{n}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={n}\left(\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} −\mathrm{2}{n}^{\mathrm{2}} −\mathrm{2}{n}−\mathrm{2}{n}−\mathrm{2}+\mathrm{3}{n}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={n}\left(\mathrm{2}{n}^{\mathrm{3}} −{n}\right)={n}^{\mathrm{2}} \left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${n}^{\mathrm{2}} \left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{8128} \\ $$$$\Rightarrow{a}\left(\mathrm{2}{a}−\mathrm{1}\right)=\mathrm{8128} \\ $$$$\Rightarrow\mathrm{2}{a}^{\mathrm{2}} −{a}−\mathrm{8128}=\mathrm{0} \\ $$$${a}=\mathrm{64} \\ $$$${n}=\mathrm{8} \\ $$$${T}_{{n}} =\left(\mathrm{2}{n}−\mathrm{1}\right)=\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *