Menu Close

find-the-value-of-S-n-k-0-k-n-1-k-C-n-k-2k-1-

Tinku Tara 0 Comments
Pin




Question Number 27380 by abdo imad last updated on 05/Jan/18
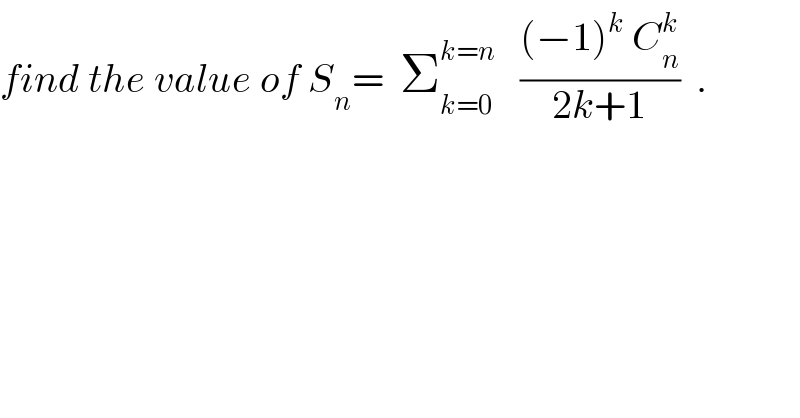
find the value of S_n = Σ_(k=0) ^(k=n) (((−1)^k C_n ^k )/(2k+1)) .
$${find}\:{the}\:{value}\:{of}\:{S}_{{n}} =\:\:\sum_{{k}=\mathrm{0}} ^{{k}={n}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\:\:. \\ $$
Commented by abdo imad last updated on 07/Jan/18
let introduce the polynomial p(x)= Σ_(k=0) ^(k=n) (((−1)^k C_n ^k )/(2k+1)) x^(2k+1) S_n =p(1) we have p^, (x)= Σ_(k=0) ^n C_n ^k (−1)^k x^(2k) = Σ_(k=0) ^(k=n) C_n ^k (−x^2 )^k = (1−x^2 )^n p(x)= ∫_0 ^x (1−t^2 )^n dt +λ and λ=p(0)=0 S_n = ∫_0 ^1 (1−t^2 )^n dt and the ch. t=sinx give S_n = ∫_0 ^(π/2) (1−sin^2 x)^n cosxdx=∫_0 ^(π/2) cosx^(2n+1) dx let put I_n = ∫_0 ^(π/2) (cosx)^n dx (wallis integral) integration by parts give I_n = ((n−1)/n) I_(n−2) ⇒ I_(2n+1) = ((2n)/(2n+1)) I_(2n−1) Π_(k=1) ^n I_(2k+1) = Π_(k=1) ^n ((2k)/(2k+1)) Π_(k=1) ^n I_(2k−1) ⇒ I_(2n+1) = ((2^n (n!))/(3.5....(2n+1))) I_1 but I_1 = 1 S_n = ((2^(2n) (n!)^2 )/((2n+1)!)).
$${let}\:{introduce}\:{the}\:{polynomial}\:{p}\left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{k}={n}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\:{x}^{\mathrm{2}{k}+\mathrm{1}} \\ $$$${S}_{{n}} ={p}\left(\mathrm{1}\right)\:\:{we}\:{have}\:{p}^{,} \left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}} \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{{k}={n}} \:{C}_{{n}} ^{{k}} \:\left(−{x}^{\mathrm{2}} \right)^{{k}} =\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} \: \\ $$$${p}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} {dt}\:+\lambda\:\:{and}\:\lambda={p}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${S}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} {dt}\:\:{and}\:{the}\:{ch}.\:{t}={sinx}\:{give} \\ $$$${S}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)^{{n}} {cosxdx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosx}^{\mathrm{2}{n}+\mathrm{1}} {dx}\:\:\:{let}\:{put} \\ $$$${I}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cosx}\right)^{{n}} {dx}\:\:\left({wallis}\:{integral}\right)\:{integration}\:{by}\:{parts}\: \\ $$$${give}\:{I}_{{n}} =\:\frac{{n}−\mathrm{1}}{{n}}\:{I}_{{n}−\mathrm{2}} \:\:\:\Rightarrow\:\:{I}_{\mathrm{2}{n}+\mathrm{1}} =\:\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}\:{I}_{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\prod_{{k}=\mathrm{1}} ^{{n}} \:{I}_{\mathrm{2}{k}+\mathrm{1}} =\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{1}}\:\prod_{{k}=\mathrm{1}} ^{{n}} \:{I}_{\mathrm{2}{k}−\mathrm{1}} \\ $$$$\Rightarrow\:{I}_{\mathrm{2}{n}+\mathrm{1}} =\:\frac{\mathrm{2}^{{n}} \:\left({n}!\right)}{\mathrm{3}.\mathrm{5}….\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{I}_{\mathrm{1}} \:\:\:\:{but}\:\:{I}_{\mathrm{1}} =\:\mathrm{1} \\ $$$${S}_{{n}} \:\:=\:\frac{\mathrm{2}^{\mathrm{2}{n}} \:\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *