Question Number 182875 by HeferH last updated on 15/Dec/22
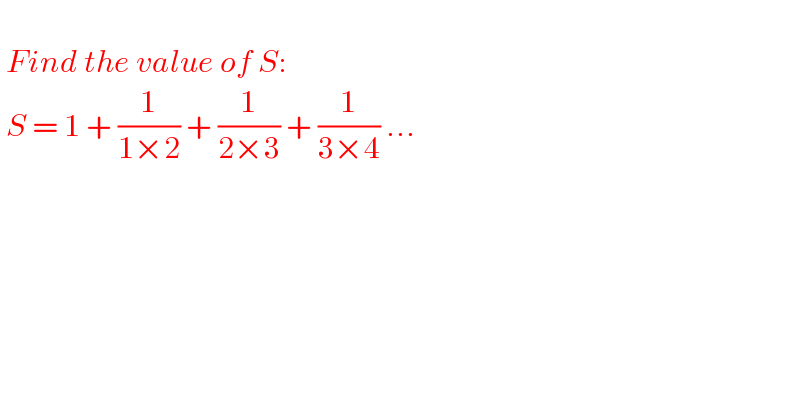
$$ \\ $$$$\:{Find}\:{the}\:{value}\:{of}\:{S}: \\ $$$$\:{S}\:=\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}\:… \\ $$$$\: \\ $$
Answered by TheSupreme last updated on 16/Dec/22
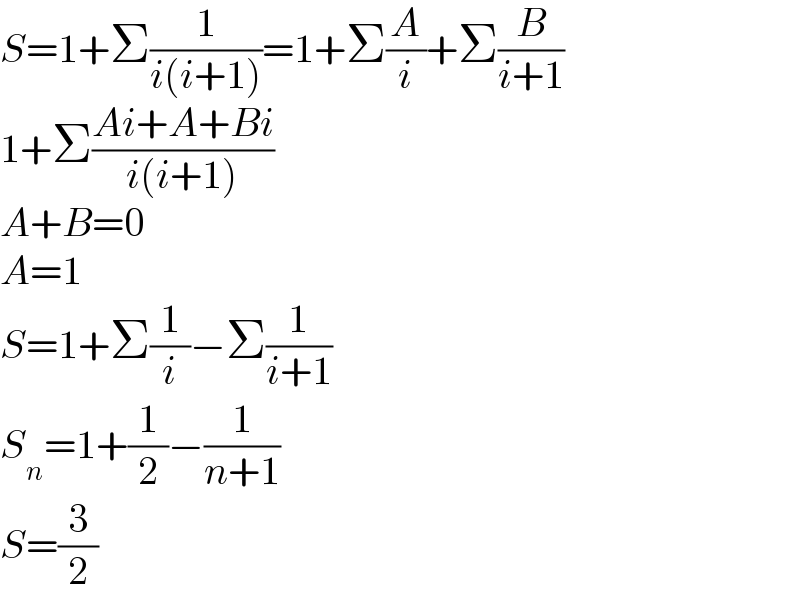
$${S}=\mathrm{1}+\Sigma\frac{\mathrm{1}}{{i}\left({i}+\mathrm{1}\right)}=\mathrm{1}+\Sigma\frac{{A}}{{i}}+\Sigma\frac{{B}}{{i}+\mathrm{1}} \\ $$$$\mathrm{1}+\Sigma\frac{{Ai}+{A}+{Bi}}{{i}\left({i}+\mathrm{1}\right)} \\ $$$${A}+{B}=\mathrm{0} \\ $$$${A}=\mathrm{1} \\ $$$${S}=\mathrm{1}+\Sigma\frac{\mathrm{1}}{{i}}−\Sigma\frac{\mathrm{1}}{{i}+\mathrm{1}} \\ $$$${S}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${S}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Frix last updated on 16/Dec/22
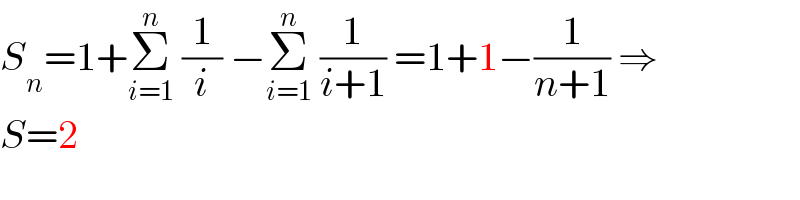
$${S}_{{n}} =\mathrm{1}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{i}}\:−\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{i}+\mathrm{1}}\:=\mathrm{1}+\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$${S}=\mathrm{2} \\ $$
Answered by manxsol last updated on 16/Dec/22
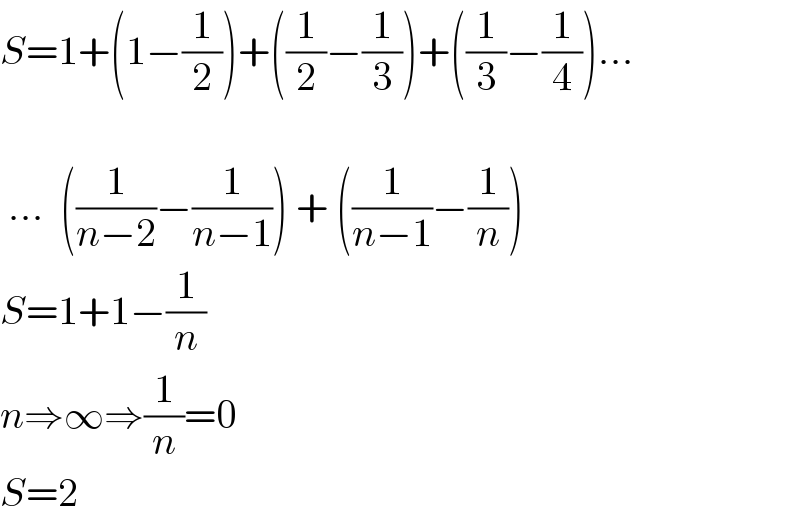
$${S}=\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}\right)… \\ $$$$ \\ $$$$\:…\:\:\left(\frac{\mathrm{1}}{{n}−\mathrm{2}}−\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)\:+\:\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right) \\ $$$${S}=\mathrm{1}+\mathrm{1}−\frac{\mathrm{1}}{{n}} \\ $$$${n}\Rightarrow\infty\Rightarrow\frac{\mathrm{1}}{{n}}=\mathrm{0} \\ $$$${S}=\mathrm{2} \\ $$
