Question Number 108222 by ZiYangLee last updated on 15/Aug/20

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{tan6}°\mathrm{tan42}°\mathrm{tan66}°\mathrm{tan78}°\:\mathrm{without} \\ $$$$\mathrm{calculator}. \\ $$
Answered by Dwaipayan Shikari last updated on 15/Aug/20
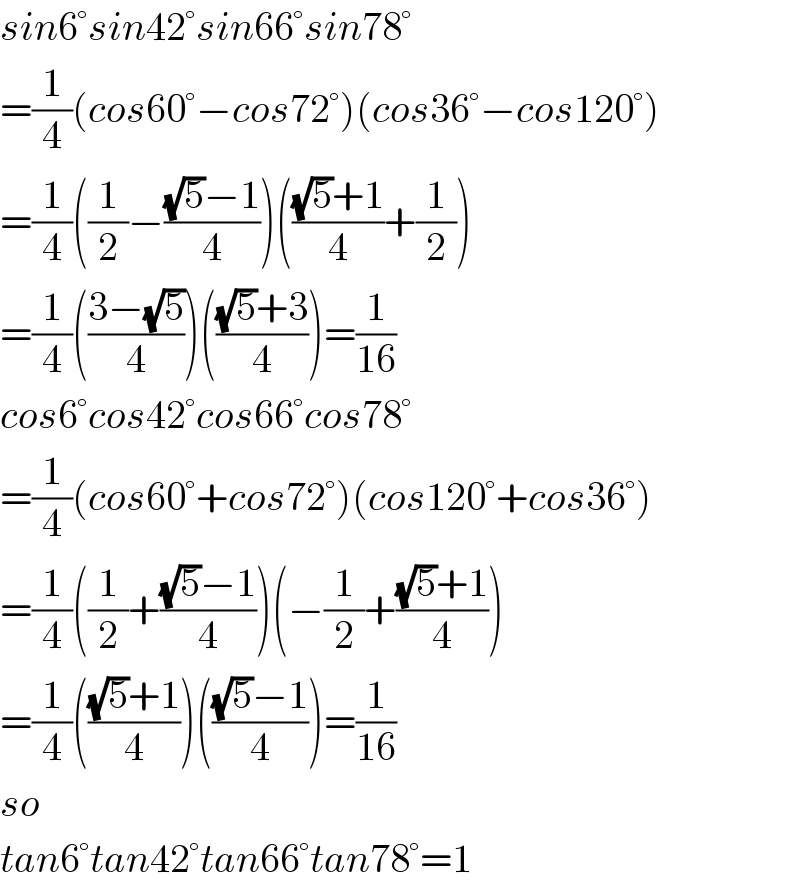
$${sin}\mathrm{6}°{sin}\mathrm{42}°{sin}\mathrm{66}°{sin}\mathrm{78}° \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({cos}\mathrm{60}°−{cos}\mathrm{72}°\right)\left({cos}\mathrm{36}°−{cos}\mathrm{120}°\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\left(\frac{\sqrt{\mathrm{5}}+\mathrm{3}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${cos}\mathrm{6}°{cos}\mathrm{42}°{cos}\mathrm{66}°{cos}\mathrm{78}° \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({cos}\mathrm{60}°+{cos}\mathrm{72}°\right)\left({cos}\mathrm{120}°+{cos}\mathrm{36}°\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${so} \\ $$$${tan}\mathrm{6}°{tan}\mathrm{42}°{tan}\mathrm{66}°{tan}\mathrm{78}°=\mathrm{1} \\ $$
