Question Number 46473 by peter frank last updated on 27/Oct/18
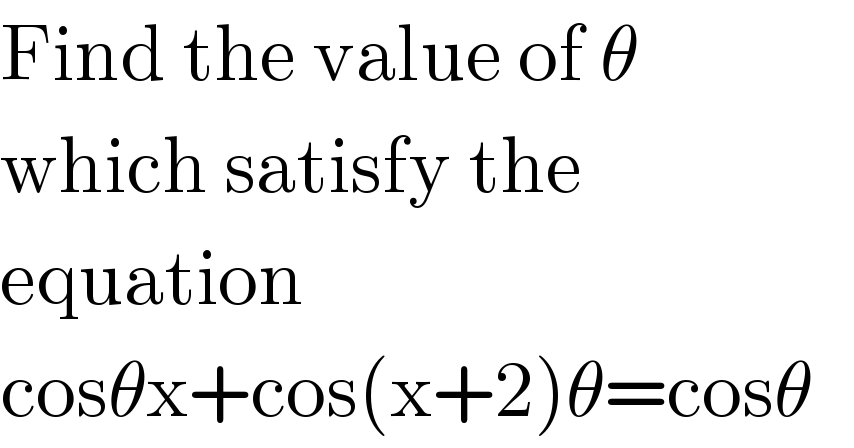
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\theta \\ $$$$\mathrm{which}\:\mathrm{satisfy}\:\mathrm{the}\: \\ $$$$\mathrm{equation} \\ $$$$\mathrm{cos}\theta\mathrm{x}+\mathrm{cos}\left(\mathrm{x}+\mathrm{2}\right)\theta=\mathrm{cos}\theta \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Oct/18
![2cos(((xθ+xθ+2θ)/2))cos(((xθ+2θ−xθ)/2))=cosθ 2cos(xθ+θ)cosθ−cosθ=0 cosθ{2cos(xθ+θ)−1}=0 either cosθ=0 cosθ=cos(π/2) so θ=2nπ±(π/2) or cos(xθ+θ)=(1/2)=cos(π/3) θ(x+1)=2nπ±(π/3) θ=(1/(x+1))[2nπ±(π/3)]](https://www.tinkutara.com/question/Q46479.png)
$$\mathrm{2}{cos}\left(\frac{{x}\theta+{x}\theta+\mathrm{2}\theta}{\mathrm{2}}\right){cos}\left(\frac{{x}\theta+\mathrm{2}\theta−{x}\theta}{\mathrm{2}}\right)={cos}\theta \\ $$$$\mathrm{2}{cos}\left({x}\theta+\theta\right){cos}\theta−{cos}\theta=\mathrm{0} \\ $$$${cos}\theta\left\{\mathrm{2}{cos}\left({x}\theta+\theta\right)−\mathrm{1}\right\}=\mathrm{0} \\ $$$${either}\:{cos}\theta=\mathrm{0}\:\:{cos}\theta={cos}\frac{\pi}{\mathrm{2}} \\ $$$${so}\:\theta=\mathrm{2}{n}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$${or}\:{cos}\left({x}\theta+\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}={cos}\frac{\pi}{\mathrm{3}} \\ $$$$\theta\left({x}+\mathrm{1}\right)=\mathrm{2}{n}\pi\pm\frac{\pi}{\mathrm{3}} \\ $$$$\theta=\frac{\mathrm{1}}{{x}+\mathrm{1}}\left[\mathrm{2}{n}\pi\pm\frac{\pi}{\mathrm{3}}\right] \\ $$
