Question Number 128780 by bramlexs22 last updated on 10/Jan/21
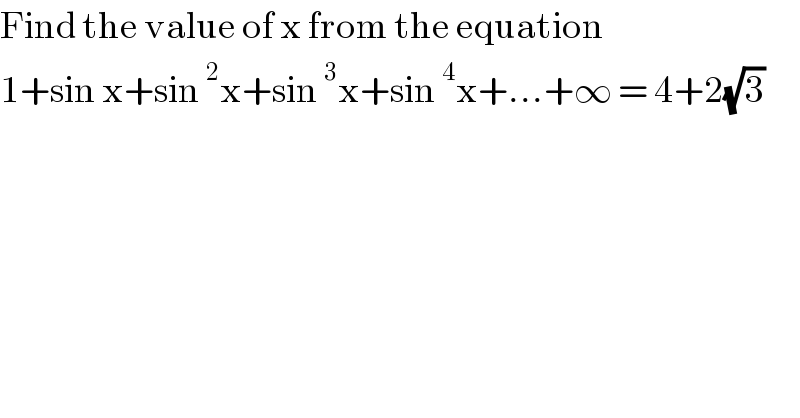
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{from}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{1}+\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}+…+\infty\:=\:\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$
Answered by liberty last updated on 10/Jan/21

$$\:\mathrm{Its}\:\mathrm{GP}\:\mathrm{with}\:\begin{cases}{\mathrm{T}_{\mathrm{1}} =\mathrm{1}}\\{\mathrm{ratio}\:=\:\mathrm{sin}\:\mathrm{x}}\end{cases} \\ $$$$\:\mathrm{we}\:\mathrm{get}\:\mathrm{T}_{\infty} \:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\:=\:\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\:\:\mathrm{1}−\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}\:;\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1}−\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}\:} \\ $$$$\:\:\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}}\:;\:\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\: \\ $$$$\:\begin{cases}{\mathrm{x}\:=\:\frac{\pi}{\mathrm{3}}+\mathrm{2n}\pi}\\{\mathrm{x}=\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2n}\pi}\end{cases}\:\mathrm{for}\:\mathrm{n}\:\in\:\mathbb{Z}\: \\ $$$$\: \\ $$
