Question Number 14879 by Tinkutara last updated on 05/Jun/17
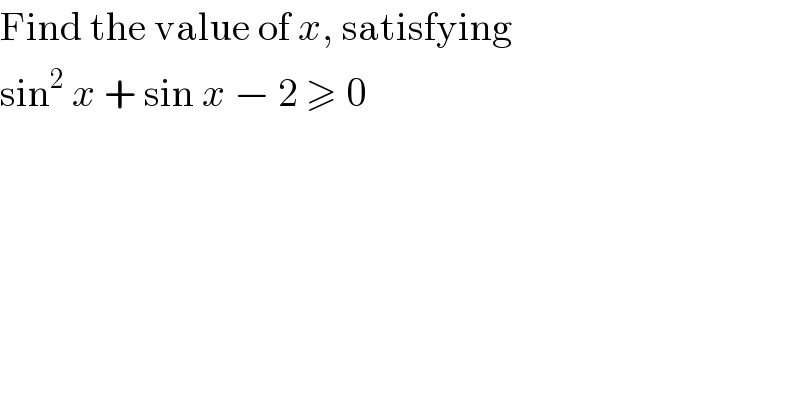
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x},\:\mathrm{satisfying} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\:+\:\mathrm{sin}\:{x}\:−\:\mathrm{2}\:\geqslant\:\mathrm{0} \\ $$
Answered by ajfour last updated on 05/Jun/17
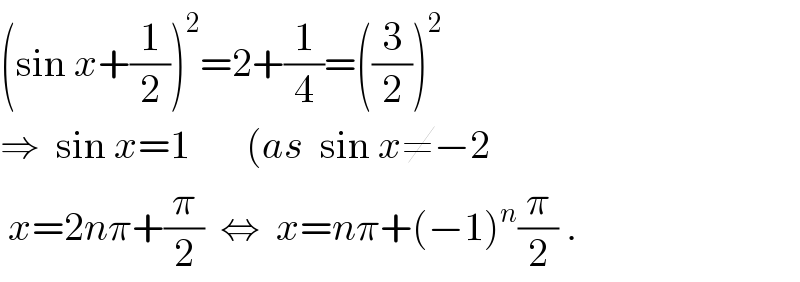
$$\left(\mathrm{sin}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:{x}=\mathrm{1}\:\:\:\:\:\:\:\left({as}\:\:\mathrm{sin}\:{x}\neq−\mathrm{2}\right. \\ $$$$\:{x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{2}}\:\:\Leftrightarrow\:\:{x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \frac{\pi}{\mathrm{2}}\:. \\ $$
Commented by Tinkutara last updated on 05/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
