Question Number 33232 by prof Abdo imad last updated on 13/Apr/18
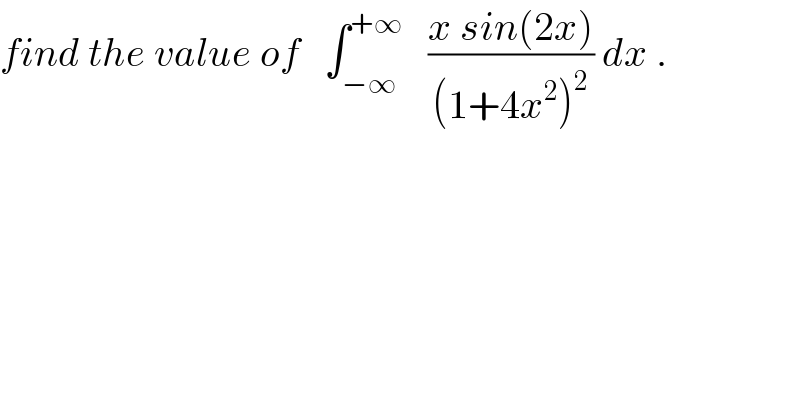
$${find}\:{the}\:{value}\:{of}\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}\:{sin}\left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:. \\ $$
Commented by prof Abdo imad last updated on 15/Apr/18
![let put I = ∫_(−∞) ^(+∞) ((x sinx)/((1+4x^2 )^2 ))dx I =−(1/8) ∫_(−∞) ^(+∞) (((−8x)/((1+4x^2 )^2 ))) sin(2x)dx by psrts u^′ = ((−8x)/((1+4x^2 ))) and v(x)=sin(2x) ⇒ −8 I = [ (1/((1+4x^2 ))) sin(2x)]_(−∞) ^(+∞) −∫_(−∞) ^(+∞) (1/(1+4x^2 ))2 cos(2x)dx =−2 ∫_(−∞) ^(+∞) ((cos(2x))/(1+4x^2 ))dx ⇒ I =(1/4) ∫_(−∞) ^(+∞) ((cos(2x))/(1+4x^2 ))dx ∫_(−∞) ^(+∞) ((cos(2x))/(1+4x^2 ))dx =Re( ∫_(−∞) ^(+∞) (e^(i2x) /(1+4x^2 ))dx) let introduce the complex finction ϕ(z) = (e^(2iz) /(1+4z^2 )) we have ϕ(z) = (e^(2iz) /((2z−i)(2z+i))) = (e^(2iz) /(4( z −(i/2))(z+(i/2)))) so the poles of ϕ are (i/2) and −(i/2) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,(i/2)) Res(ϕ,(i/2)) = lim_(z→(i/2)) (z−(i/2))ϕ(z) = (e^(2i(i/2)) /(4(2(i/2))))= (e^(−1) /(4i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ .(e^(−1) /(4i)) = (π/(2e)) ⇒ I =(1/4) (π/(2e)) ⇒ I = (π/(8e)) .](https://www.tinkutara.com/question/Q33392.png)
$${let}\:{put}\:\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{x}\:{sinx}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$${I}\:\:=−\frac{\mathrm{1}}{\mathrm{8}}\:\int_{−\infty} ^{+\infty} \:\:\left(\frac{−\mathrm{8}{x}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)\:{sin}\left(\mathrm{2}{x}\right){dx}\:{by}\:{psrts} \\ $$$${u}^{'} \:\:=\:\frac{−\mathrm{8}{x}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)}\:{and}\:{v}\left({x}\right)={sin}\left(\mathrm{2}{x}\right)\:\Rightarrow \\ $$$$−\mathrm{8}\:{I}\:=\:\left[\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} \right)}\:{sin}\left(\mathrm{2}{x}\right)\right]_{−\infty} ^{+\infty} \:−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\mathrm{2}\:{cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$=−\mathrm{2}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\:={Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{{i}\mathrm{2}{x}} }{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:{introduce}\:{the}\:{complex}\:{finction} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{\mathrm{2}{iz}} }{\mathrm{1}+\mathrm{4}{z}^{\mathrm{2}} }\:\:{we}\:{have}\:\varphi\left({z}\right)\:=\:\frac{{e}^{\mathrm{2}{iz}} }{\left(\mathrm{2}{z}−{i}\right)\left(\mathrm{2}{z}+{i}\right)} \\ $$$$=\:\frac{{e}^{\mathrm{2}{iz}} }{\mathrm{4}\left(\:{z}\:−\frac{{i}}{\mathrm{2}}\right)\left({z}+\frac{{i}}{\mathrm{2}}\right)}\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\frac{{i}}{\mathrm{2}}\:{and} \\ $$$$−\frac{{i}}{\mathrm{2}}\:\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\frac{{i}}{\mathrm{2}}\right) \\ $$$${Res}\left(\varphi,\frac{{i}}{\mathrm{2}}\right)\:=\:{lim}_{{z}\rightarrow\frac{{i}}{\mathrm{2}}} \left({z}−\frac{{i}}{\mathrm{2}}\right)\varphi\left({z}\right) \\ $$$$=\:\:\frac{{e}^{\mathrm{2}{i}\frac{{i}}{\mathrm{2}}} }{\mathrm{4}\left(\mathrm{2}\frac{{i}}{\mathrm{2}}\right)}=\:\:\frac{{e}^{−\mathrm{1}} }{\mathrm{4}{i}}\:\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:.\frac{{e}^{−\mathrm{1}} }{\mathrm{4}{i}} \\ $$$$=\:\frac{\pi}{\mathrm{2}{e}}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{\mathrm{2}{e}}\:\Rightarrow\:\:{I}\:=\:\frac{\pi}{\mathrm{8}{e}}\:. \\ $$$$ \\ $$
