Find-the-value-s-of-a-such-that-a-x-ax-with-a-x-R-

Question Number 45982 by MrW3 last updated on 19/Oct/18

F i n d t h e v a l u e (s) o f a s u c h t h a t

a^{x} ⩾ a x w i t h a, x \in R .

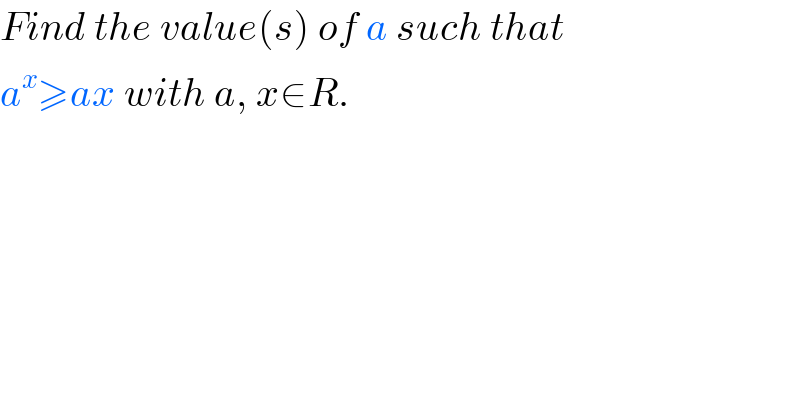
Commented by ajfour last updated on 19/Oct/18

Answered by ajfour last updated on 19/Oct/18

\underset{- - - - - - -}{F o r x ⩾ 1}

x ⩾ 1 + \ln_{a} x

\ln_{a} x ⩽ x - 1

\ln x ⩽ (\ln a) (x - 1)

\Rightarrow \frac{1}{x} ∣_{x = 1} ⩽ \ln a \Rightarrow a ⩾ e

\underset{- - - - - -}{F o r x ⩽ 1}

\ln x ⩽ (\ln a) (x - 1)

\Rightarrow \frac{d}{d x} (\ln x) ∣_{x = 1} ⩾ \ln a

\Rightarrow \ln a ⩽ 1 \Rightarrow a ⩽ e

H e n c e f o r a l l x \in R, a > 0

a^{x} ⩾ a x i f a = e .

Commented by ajfour last updated on 19/Oct/18

p l e a s e c h e c k a g a i n S i r, i h a v e

e d i t e d t h o u g h i h a v e n o t

e x p l a i n e d . .

Commented by MrW3 last updated on 19/Oct/18

{t h a t}^{'} s p e r f e c t s i r! t h a n k s a l o t!

Facebook Tweet Pin