Question Number 114122 by bemath last updated on 17/Sep/20
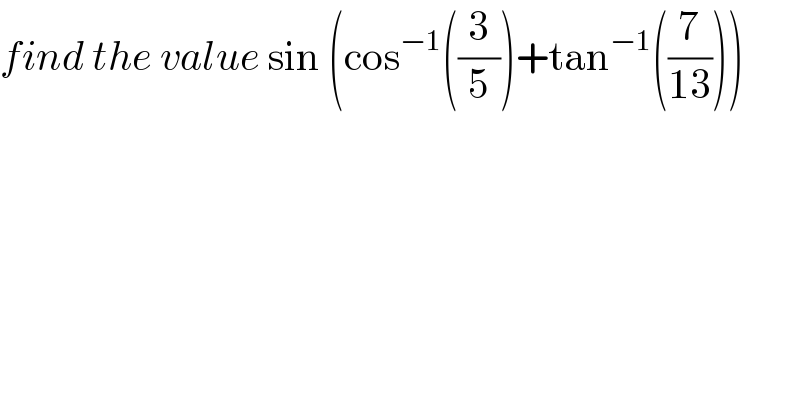
$${find}\:{the}\:{value}\:\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}}{\mathrm{13}}\right)\right) \\ $$
Answered by mr W last updated on 17/Sep/20

$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{13}}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{7}}{\:\sqrt{\mathrm{218}}}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{13}}{\:\sqrt{\mathrm{218}}} \\ $$$$\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{sin}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}}{\mathrm{13}}\right)\right) \\ $$$$=\left(\mathrm{sin}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}\right)\:\left(\mathrm{cos}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{13}}\right)+\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}\right)\:\mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}}{\mathrm{13}}\right) \\ $$$$=\left(\mathrm{sin}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}\right)\:\left(\mathrm{cos}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{13}}{\:\sqrt{\mathrm{218}}}\right)+\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}\right)\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{7}}{\:\sqrt{\mathrm{218}}}\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{13}}{\:\sqrt{\mathrm{218}}}+\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{7}}{\:\sqrt{\mathrm{218}}} \\ $$$$=\frac{\mathrm{73}}{\:\mathrm{5}\sqrt{\mathrm{218}}} \\ $$
Commented by bemath last updated on 17/Sep/20

$${santuyy} \\ $$
