Question Number 39373 by maxmathsup by imad last updated on 05/Jul/18
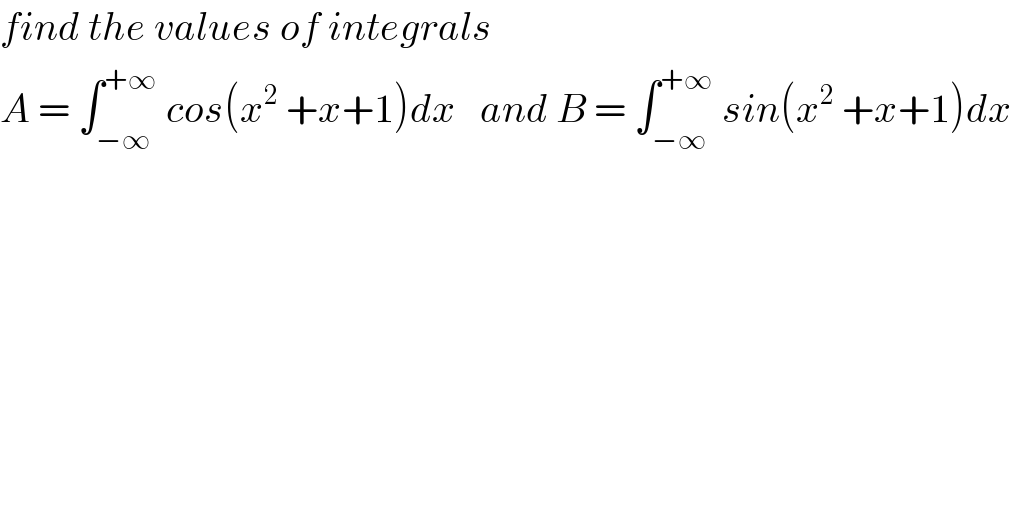
$${find}\:{the}\:{values}\:{of}\:{integrals} \\ $$$${A}\:=\:\int_{−\infty} ^{+\infty} \:{cos}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right){dx}\:\:\:{and}\:{B}\:=\:\int_{−\infty} ^{+\infty} \:{sin}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right){dx} \\ $$
Commented by math khazana by abdo last updated on 06/Jul/18
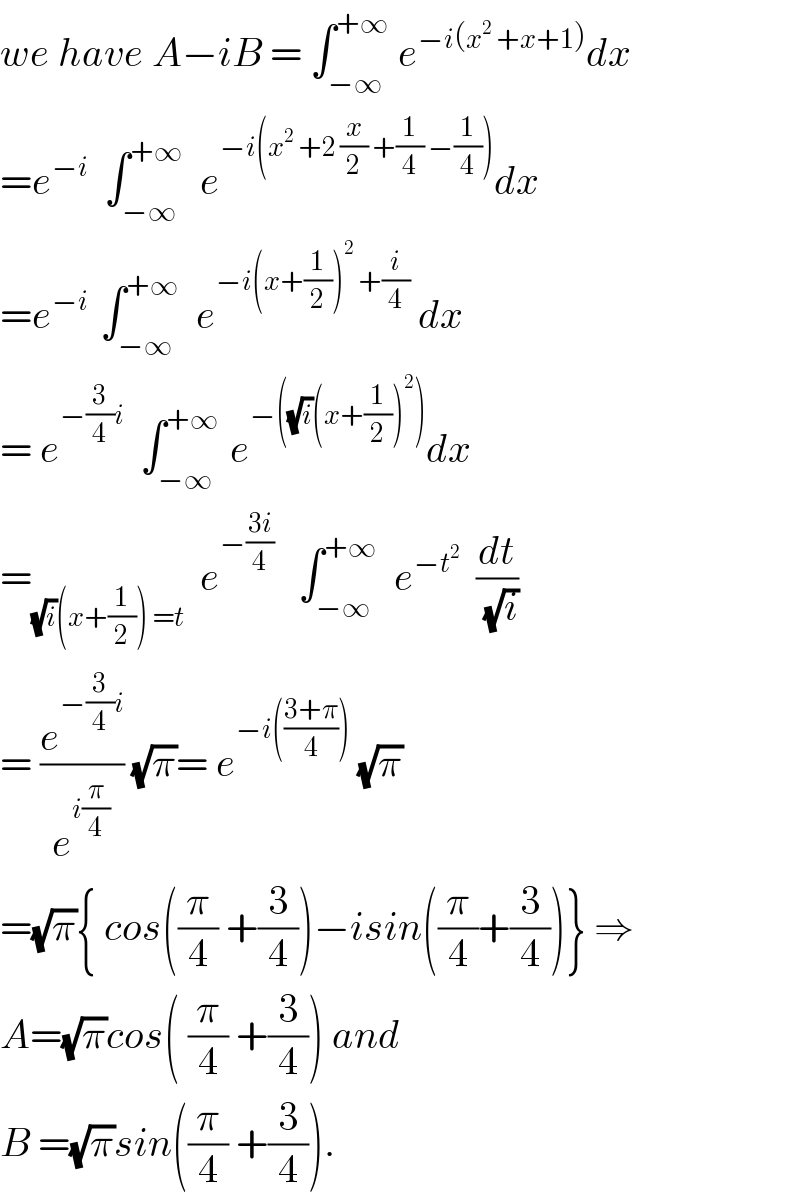
$${we}\:{have}\:{A}−{iB}\:=\:\int_{−\infty} ^{+\infty} \:{e}^{−{i}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)} {dx} \\ $$$$={e}^{−{i}} \:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{i}\left({x}^{\mathrm{2}} \:+\mathrm{2}\:\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{4}}\right)} {dx} \\ $$$$={e}^{−{i}\:} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−{i}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{{i}}{\mathrm{4}}} \:{dx} \\ $$$$=\:{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}} \:\:\int_{−\infty} ^{+\infty\:} \:{e}^{−\left(\sqrt{{i}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)} {dx} \\ $$$$=_{\sqrt{{i}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:={t}} \:\:{e}^{−\frac{\mathrm{3}{i}}{\mathrm{4}}} \:\:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{t}^{\mathrm{2}} } \:\:\frac{{dt}}{\:\sqrt{{i}}} \\ $$$$=\:\frac{{e}^{−\frac{\mathrm{3}}{\mathrm{4}}{i}} }{{e}^{{i}\frac{\pi}{\mathrm{4}}} }\:\sqrt{\pi}=\:{e}^{−{i}\left(\frac{\mathrm{3}+\pi}{\mathrm{4}}\right)} \:\sqrt{\pi} \\ $$$$=\sqrt{\pi}\left\{\:{cos}\left(\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\right)−{isin}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}\right)\right\}\:\Rightarrow \\ $$$${A}=\sqrt{\pi}{cos}\left(\:\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\right)\:{and} \\ $$$${B}\:=\sqrt{\pi}{sin}\left(\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{3}}{\mathrm{4}}\right). \\ $$
