Menu Close

find-the-values-of-k-for-which-the-line-y-kx-3-does-not-meet-the-curve-y-2x-2-3x-k-

Tinku Tara 0 Comments
Pin




Question Number 113857 by ayenisamuel last updated on 15/Sep/20
find the values of k for which the line y=kx−3 does not meet the curve y=2x^2 −3x+k.
$${find}\:{the}\:{values}\:{of}\:{k}\:{for}\:{which}\:{the} \\ $$$${line}\:{y}={kx}−\mathrm{3}\:{does}\:{not}\:{meet}\:{the}\:{curve} \\ $$$${y}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k}. \\ $$
Answered by MJS_new last updated on 15/Sep/20
first, intersect them kx−3=2x^2 −3x+k x^2 −((k+3)/2)x+((k+3)/2)=0 let x=t+((k+3)/4) and solve for t^2 t^2 =(((k−5)(k+3))/(16)) ⇒ if (((k−5)(k+3))/(16))<0 ⇒ no solution ⇒ −3<k<5 is the answer
$$\mathrm{first},\:\mathrm{intersect}\:\mathrm{them} \\ $$$${kx}−\mathrm{3}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k} \\ $$$${x}^{\mathrm{2}} −\frac{{k}+\mathrm{3}}{\mathrm{2}}{x}+\frac{{k}+\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={t}+\frac{{k}+\mathrm{3}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:{t}^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} =\frac{\left({k}−\mathrm{5}\right)\left({k}+\mathrm{3}\right)}{\mathrm{16}} \\ $$$$\Rightarrow\:\mathrm{if}\:\frac{\left({k}−\mathrm{5}\right)\left({k}+\mathrm{3}\right)}{\mathrm{16}}<\mathrm{0}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\Rightarrow\:−\mathrm{3}<{k}<\mathrm{5}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer} \\ $$
Answered by 1549442205PVT last updated on 16/Sep/20
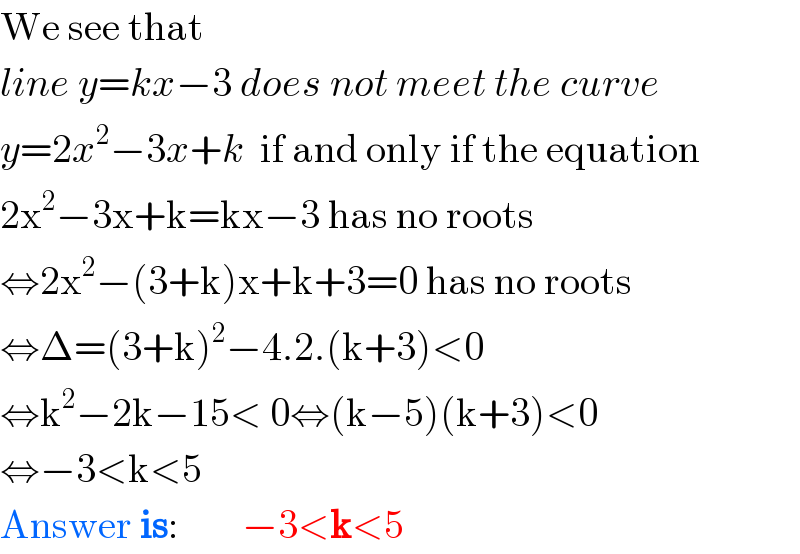
We see that line y=kx−3 does not meet the curve y=2x^2 −3x+k if and only if the equation 2x^2 −3x+k=kx−3 has no roots ⇔2x^2 −(3+k)x+k+3=0 has no roots ⇔Δ=(3+k)^2 −4.2.(k+3)<0 ⇔k^2 −2k−15< 0⇔(k−5)(k+3)<0 ⇔−3<k<5 Answer is: −3<k<5
$$\mathrm{We}\:\mathrm{see}\:\mathrm{that} \\ $$$${line}\:{y}={kx}−\mathrm{3}\:{does}\:{not}\:{meet}\:{the}\:{curve} \\ $$$${y}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}+{k}\:\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{k}=\mathrm{kx}−\mathrm{3}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} −\left(\mathrm{3}+\mathrm{k}\right)\mathrm{x}+\mathrm{k}+\mathrm{3}=\mathrm{0}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\Leftrightarrow\Delta=\left(\mathrm{3}+\mathrm{k}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{2}.\left(\mathrm{k}+\mathrm{3}\right)<\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{k}^{\mathrm{2}} −\mathrm{2k}−\mathrm{15}<\:\mathrm{0}\Leftrightarrow\left(\mathrm{k}−\mathrm{5}\right)\left(\mathrm{k}+\mathrm{3}\right)<\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{3}<\mathrm{k}<\mathrm{5} \\ $$$$\mathrm{Answer}\:\boldsymbol{\mathrm{is}}:\:\:\:\:\:\:\:\:−\mathrm{3}<\boldsymbol{\mathrm{k}}<\mathrm{5} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *