Menu Close

Find-the-values-of-x-and-y-x-2-2xy-y-2-14-equation-i-2x-2-3xy-y-2-2-equation-ii-

Tinku Tara 0 Comments
Pin




Question Number 13166 by tawa tawa last updated on 15/May/17
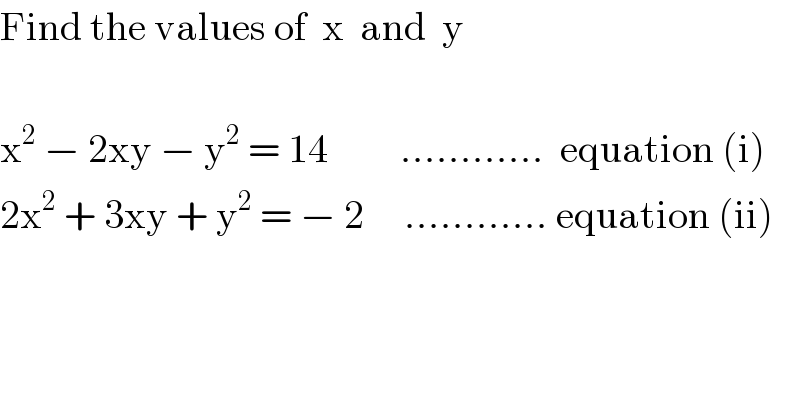
Find the values of x and y x^2 − 2xy − y^2 = 14 ............ equation (i) 2x^2 + 3xy + y^2 = − 2 ............ equation (ii)
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\:\mathrm{x}\:\:\mathrm{and}\:\:\mathrm{y} \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:−\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{14}\:\:\:\:\:\:\:\:\:…………\:\:\mathrm{equation}\:\left(\mathrm{i}\right) \\ $$$$\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{3xy}\:+\:\mathrm{y}^{\mathrm{2}} \:=\:−\:\mathrm{2}\:\:\:\:\:…………\:\mathrm{equation}\:\left(\mathrm{ii}\right) \\ $$
Answered by RasheedSindhi last updated on 16/May/17
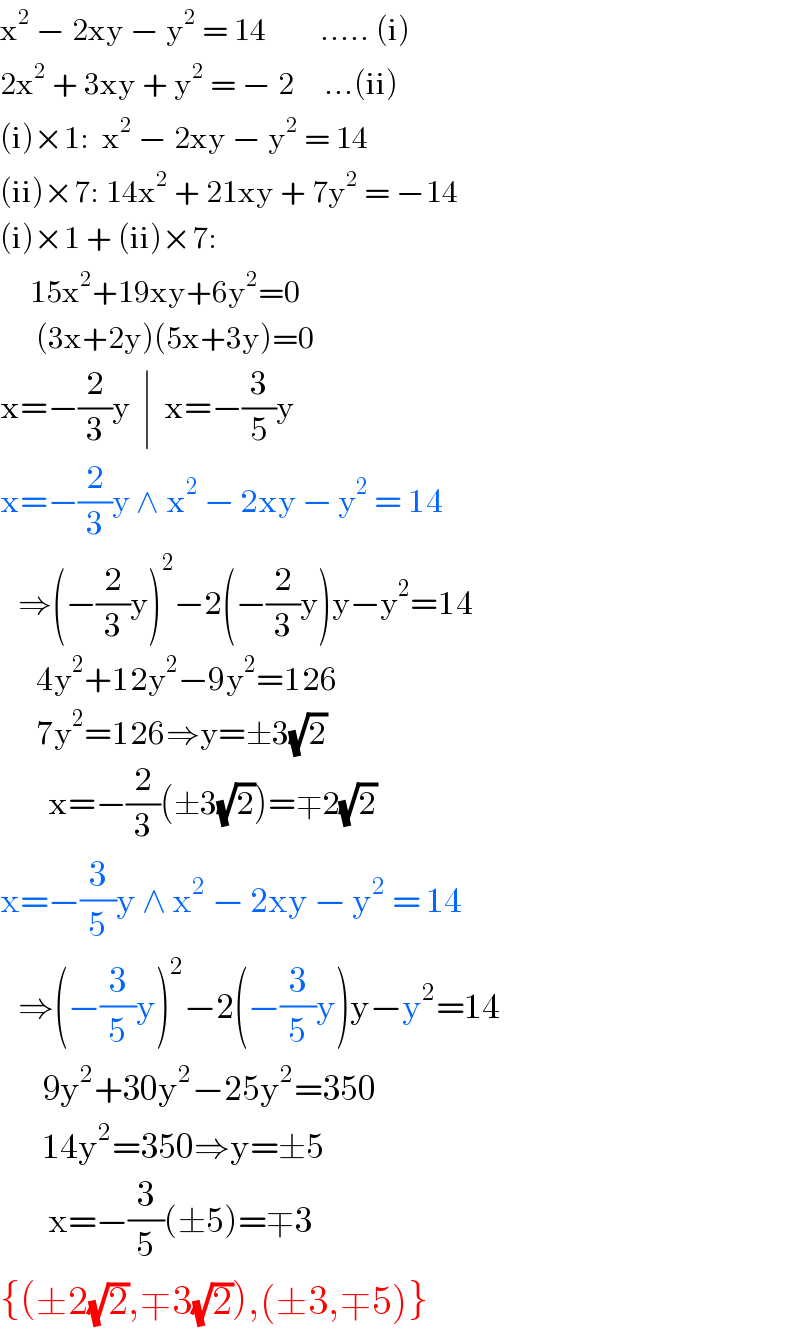
x^2 − 2xy − y^2 = 14 ..... (i) 2x^2 + 3xy + y^2 = − 2 ...(ii) (i)×1: x^2 − 2xy − y^2 = 14 (ii)×7: 14x^2 + 21xy + 7y^2 = −14 (i)×1 + (ii)×7: 15x^2 +19xy+6y^2 =0 (3x+2y)(5x+3y)=0 x=−(2/3)y ∣ x=−(3/5)y x=−(2/3)y ∧ x^2 − 2xy − y^2 = 14 ⇒(−(2/3)y)^2 −2(−(2/3)y)y−y^2 =14 4y^2 +12y^2 −9y^2 =126 7y^2 =126⇒y=±3(√2) x=−(2/3)(±3(√2))=∓2(√2) x=−(3/5)y ∧ x^2 − 2xy − y^2 = 14 ⇒(−(3/5)y)^2 −2(−(3/5)y)y−y^2 =14 9y^2 +30y^2 −25y^2 =350 14y^2 =350⇒y=±5 x=−(3/5)(±5)=∓3 {(±2(√2),∓3(√2)),(±3,∓5)}
$$\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:−\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{14}\:\:\:\:\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{3xy}\:+\:\mathrm{y}^{\mathrm{2}} \:=\:−\:\mathrm{2}\:\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)×\mathrm{1}:\:\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:−\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{14}\:\:\:\:\:\:\:\:\: \\ $$$$\left(\mathrm{ii}\right)×\mathrm{7}:\:\mathrm{14x}^{\mathrm{2}} \:+\:\mathrm{21xy}\:+\:\mathrm{7y}^{\mathrm{2}} \:=\:−\mathrm{14} \\ $$$$\left(\mathrm{i}\right)×\mathrm{1}\:+\:\left(\mathrm{ii}\right)×\mathrm{7}: \\ $$$$\:\:\:\:\:\mathrm{15x}^{\mathrm{2}} +\mathrm{19xy}+\mathrm{6y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\left(\mathrm{3x}+\mathrm{2y}\right)\left(\mathrm{5x}+\mathrm{3y}\right)=\mathrm{0} \\ $$$$\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\:\:\mid\:\:\mathrm{x}=−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{y} \\ $$$$\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\:\wedge\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:−\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{14} \\ $$$$\:\:\:\Rightarrow\left(−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2}\left(−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{y}\right)\mathrm{y}−\mathrm{y}^{\mathrm{2}} =\mathrm{14} \\ $$$$\:\:\:\:\:\:\mathrm{4y}^{\mathrm{2}} +\mathrm{12y}^{\mathrm{2}} −\mathrm{9y}^{\mathrm{2}} =\mathrm{126} \\ $$$$\:\:\:\:\:\:\mathrm{7y}^{\mathrm{2}} =\mathrm{126}\Rightarrow\mathrm{y}=\pm\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}=−\frac{\mathrm{2}}{\mathrm{3}}\left(\pm\mathrm{3}\sqrt{\mathrm{2}}\right)=\mp\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{x}=−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{y}\:\wedge\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:−\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{14} \\ $$$$\:\:\:\Rightarrow\left(−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2}\left(−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{y}\right)\mathrm{y}−\mathrm{y}^{\mathrm{2}} =\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\mathrm{9y}^{\mathrm{2}} +\mathrm{30y}^{\mathrm{2}} −\mathrm{25y}^{\mathrm{2}} =\mathrm{350} \\ $$$$\:\:\:\:\:\:\:\mathrm{14y}^{\mathrm{2}} =\mathrm{350}\Rightarrow\mathrm{y}=\pm\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}=−\frac{\mathrm{3}}{\mathrm{5}}\left(\pm\mathrm{5}\right)=\mp\mathrm{3} \\ $$$$\left\{\left(\pm\mathrm{2}\sqrt{\mathrm{2}},\mp\mathrm{3}\sqrt{\mathrm{2}}\right),\left(\pm\mathrm{3},\mp\mathrm{5}\right)\right\} \\ $$
Commented by tawa tawa last updated on 16/May/17
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
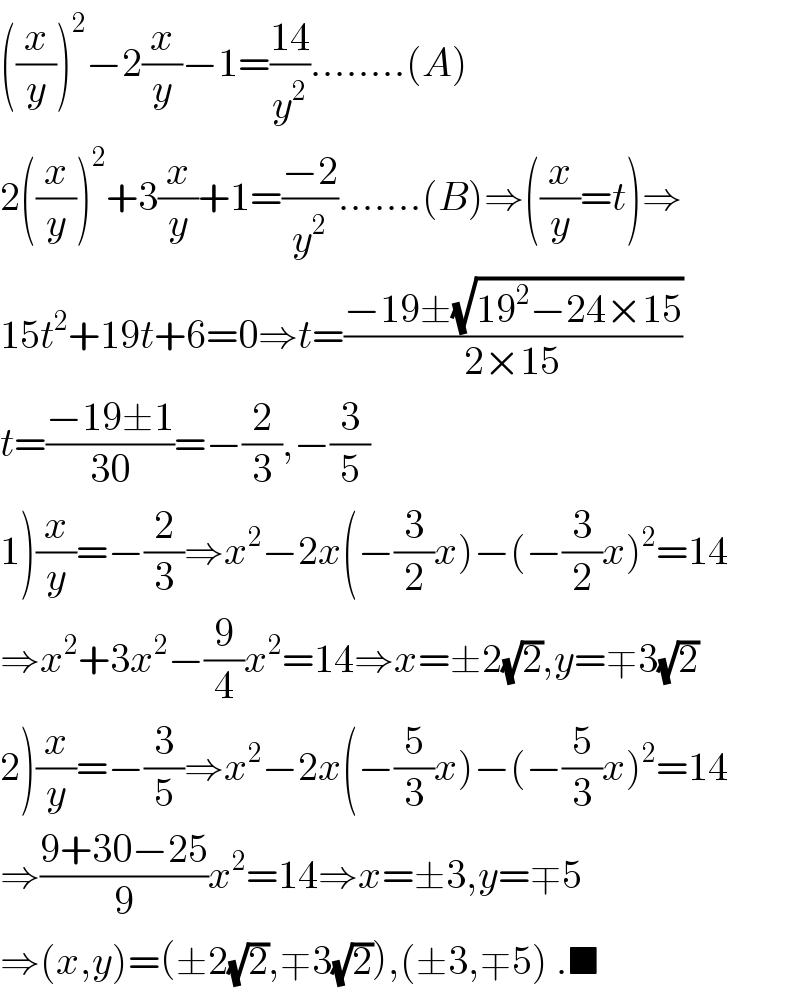
((x/y))^2 −2(x/y)−1=((14)/y^2 )........(A) 2((x/y))^2 +3(x/y)+1=((−2)/y^2 ).......(B)⇒((x/y)=t)⇒ 15t^2 +19t+6=0⇒t=((−19±(√(19^2 −24×15)))/(2×15)) t=((−19±1)/(30))=−(2/3),−(3/5) 1)(x/y)=−(2/3)⇒x^2 −2x(−(3/2)x)−(−(3/2)x)^2 =14 ⇒x^2 +3x^2 −(9/4)x^2 =14⇒x=±2(√2),y=∓3(√2) 2)(x/y)=−(3/5)⇒x^2 −2x(−(5/3)x)−(−(5/3)x)^2 =14 ⇒((9+30−25)/9)x^2 =14⇒x=±3,y=∓5 ⇒(x,y)=(±2(√2),∓3(√2)),(±3,∓5) .■
$$\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}\frac{{x}}{{y}}−\mathrm{1}=\frac{\mathrm{14}}{{y}^{\mathrm{2}} }……..\left({A}\right) \\ $$$$\mathrm{2}\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} +\mathrm{3}\frac{{x}}{{y}}+\mathrm{1}=\frac{−\mathrm{2}}{{y}^{\mathrm{2}} }…….\left({B}\right)\Rightarrow\left(\frac{{x}}{{y}}={t}\right)\Rightarrow \\ $$$$\mathrm{15}{t}^{\mathrm{2}} +\mathrm{19}{t}+\mathrm{6}=\mathrm{0}\Rightarrow{t}=\frac{−\mathrm{19}\pm\sqrt{\mathrm{19}^{\mathrm{2}} −\mathrm{24}×\mathrm{15}}}{\mathrm{2}×\mathrm{15}} \\ $$$${t}=\frac{−\mathrm{19}\pm\mathrm{1}}{\mathrm{30}}=−\frac{\mathrm{2}}{\mathrm{3}},−\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\left.\mathrm{1}\right)\frac{{x}}{{y}}=−\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}\left(−\frac{\mathrm{3}}{\mathrm{2}}{x}\right)−\left(−\frac{\mathrm{3}}{\mathrm{2}}{x}\right)^{\mathrm{2}} =\mathrm{14} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}{x}^{\mathrm{2}} =\mathrm{14}\Rightarrow{x}=\pm\mathrm{2}\sqrt{\mathrm{2}},{y}=\mp\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\frac{{x}}{{y}}=−\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}\left(−\frac{\mathrm{5}}{\mathrm{3}}{x}\right)−\left(−\frac{\mathrm{5}}{\mathrm{3}}{x}\right)^{\mathrm{2}} =\mathrm{14} \\ $$$$\Rightarrow\frac{\mathrm{9}+\mathrm{30}−\mathrm{25}}{\mathrm{9}}{x}^{\mathrm{2}} =\mathrm{14}\Rightarrow{x}=\pm\mathrm{3},{y}=\mp\mathrm{5} \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\pm\mathrm{2}\sqrt{\mathrm{2}},\mp\mathrm{3}\sqrt{\mathrm{2}}\right),\left(\pm\mathrm{3},\mp\mathrm{5}\right)\:.\blacksquare \\ $$
Commented by tawa tawa last updated on 16/May/17
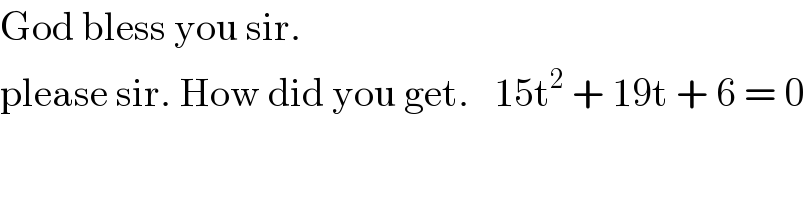
God bless you sir. please sir. How did you get. 15t^2 + 19t + 6 = 0
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$$$\mathrm{please}\:\mathrm{sir}.\:\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}.\:\:\:\mathrm{15t}^{\mathrm{2}} \:+\:\mathrm{19t}\:+\:\mathrm{6}\:=\:\mathrm{0} \\ $$
Commented by tawa tawa last updated on 16/May/17
have seen it sir. you continue ..
$$\mathrm{have}\:\mathrm{seen}\:\mathrm{it}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{continue}\:.. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
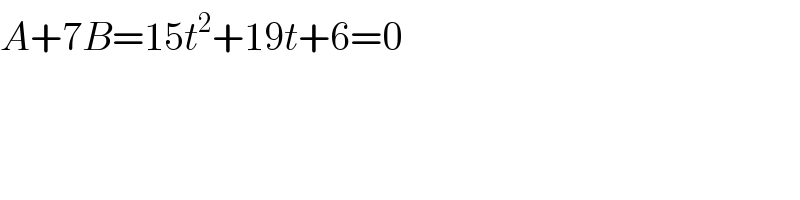
A+7B=15t^2 +19t+6=0
$${A}+\mathrm{7}{B}=\mathrm{15}{t}^{\mathrm{2}} +\mathrm{19}{t}+\mathrm{6}=\mathrm{0} \\ $$
Commented by tawa tawa last updated on 16/May/17
I understand now sir. God bless you sir
$$\mathrm{I}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *