Menu Close

Find-this-excercise-about-limits-trigonometri-1-lim-0-2cos-2-3-2-lim-x-0-1-cos-x-x-2-3-3-lim-t-0-4t-2-3t-sin-t-t-2-4-lim-x-0-x-2-1-x-cos-x-5-lim-

Tinku Tara 0 Comments
Pin




Question Number 155829 by zainaltanjung last updated on 05/Oct/21
Find this excercise about limits trigonometri 1). lim_(θ→0) ((2cos θ−2)/(3θ)) 2). lim_(x→0) ((1−cos x)/x^(2/3) ) 3). lim_(t→0) ((4t^2 +3t sin t)/t^2 ) 4). lim_(x→0) ((x^2 +1)/(x+cos x)) 5). lim_(x→0) ((sin^2 ((x/2)))/(sin x))
$$\mathrm{Find}\:\mathrm{this}\:\mathrm{excercise}\:\mathrm{about}\:\mathrm{limits} \\ $$$$\mathrm{trigonometri} \\ $$$$\left.\mathrm{1}\right).\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\theta−\mathrm{2}}{\mathrm{3}\theta} \\ $$$$\left.\mathrm{2}\right).\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}{\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$\left.\mathrm{3}\right).\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4t}^{\mathrm{2}} +\mathrm{3t}\:\mathrm{sin}\:\mathrm{t}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right).\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}+\mathrm{cos}\:\mathrm{x}} \\ $$$$\left.\mathrm{5}\right).\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{sin}\:^{\mathrm{2}} \:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{sin}\:\:\mathrm{x}} \\ $$$$ \\ $$
Commented by yeti123 last updated on 05/Oct/21
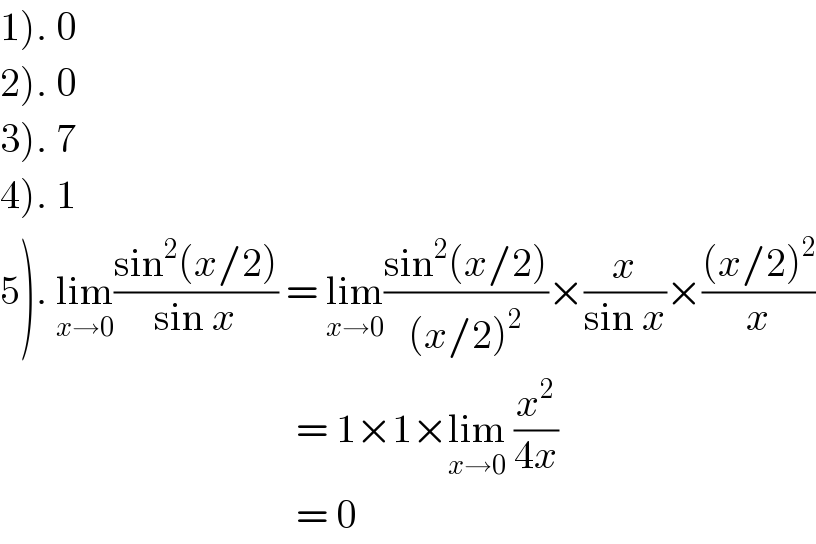
1). 0 2). 0 3). 7 4). 1 5). lim_(x→0) ((sin^2 (x/2))/(sin x)) = lim_(x→0) ((sin^2 (x/2))/((x/2)^2 ))×(x/(sin x))×(((x/2)^2 )/x) = 1×1×lim_(x→0) (x^2 /(4x)) = 0
$$\left.\mathrm{1}\right).\:\mathrm{0} \\ $$$$\left.\mathrm{2}\right).\:\mathrm{0} \\ $$$$\left.\mathrm{3}\right).\:\mathrm{7} \\ $$$$\left.\mathrm{4}\right).\:\mathrm{1} \\ $$$$\left.\mathrm{5}\right).\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{2}} \left({x}/\mathrm{2}\right)}{\mathrm{sin}\:{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{2}} \left({x}/\mathrm{2}\right)}{\left({x}/\mathrm{2}\right)^{\mathrm{2}} }×\frac{{x}}{\mathrm{sin}\:{x}}×\frac{\left({x}/\mathrm{2}\right)^{\mathrm{2}} }{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}×\mathrm{1}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{\mathrm{4}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{0} \\ $$
Commented by aliyn last updated on 05/Oct/21
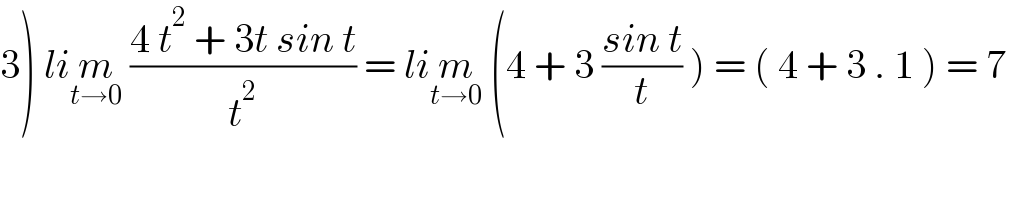
3) lim_(t→0) ((4 t^2 + 3t sin t)/t^2 ) = lim_(t→0) (4 + 3 ((sin t)/t) ) = ( 4 + 3 . 1 ) = 7
$$\left.\mathrm{3}\right)\:{li}\underset{{t}\rightarrow\mathrm{0}} {{m}}\:\frac{\mathrm{4}\:{t}^{\mathrm{2}} \:+\:\mathrm{3}{t}\:{sin}\:{t}}{{t}^{\mathrm{2}} }\:=\:{li}\underset{{t}\rightarrow\mathrm{0}} {{m}}\:\left(\mathrm{4}\:+\:\mathrm{3}\:\frac{{sin}\:{t}}{{t}}\:\right)\:=\:\left(\:\mathrm{4}\:+\:\mathrm{3}\:.\:\mathrm{1}\:\right)\:=\:\mathrm{7}\: \\ $$
Answered by Rasheed.Sindhi last updated on 05/Oct/21
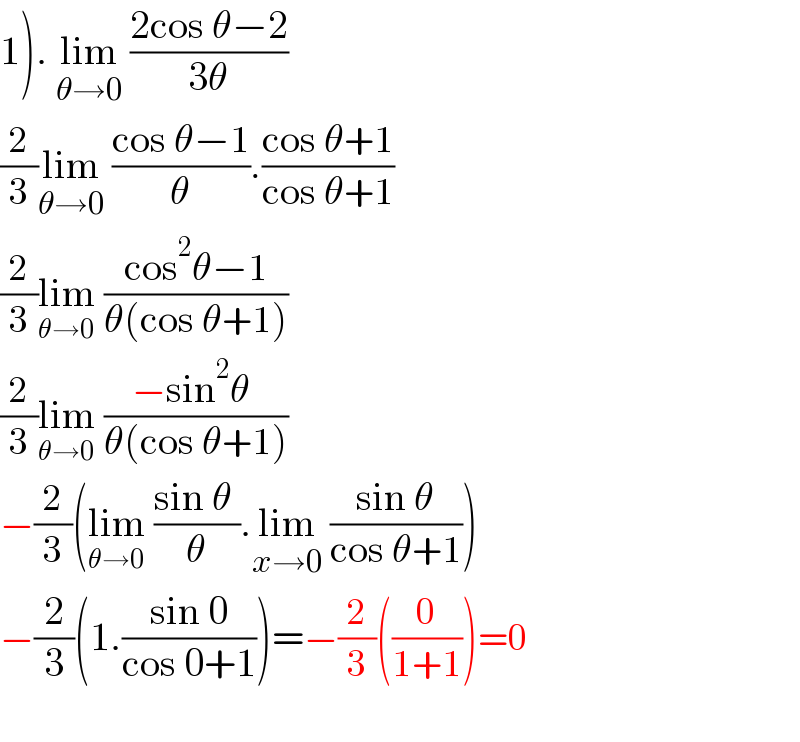
1). lim_(θ→0) ((2cos θ−2)/(3θ)) (2/3)lim_(θ→0) ((cos θ−1)/θ).((cos θ+1)/(cos θ+1)) (2/3)lim_(θ→0) ((cos^2 θ−1)/(θ(cos θ+1))) (2/3)lim_(θ→0) ((−sin^2 θ )/(θ(cos θ+1))) −(2/3)(lim_(θ→0) ((sin θ )/θ).lim_(x→0) ((sin θ)/(cos θ+1))) −(2/3)(1.((sin 0)/(cos 0+1)))=−(2/3)((0/(1+1)))=0
$$\left.\mathrm{1}\right).\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2cos}\:\theta−\mathrm{2}}{\mathrm{3}\theta} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\theta−\mathrm{1}}{\theta}.\frac{\mathrm{cos}\:\theta+\mathrm{1}}{\mathrm{cos}\:\theta+\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{1}}{\theta\left(\mathrm{cos}\:\theta+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}^{\mathrm{2}} \theta\:}{\theta\left(\mathrm{cos}\:\theta+\mathrm{1}\right)} \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}\left(\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\theta\:}{\theta}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta+\mathrm{1}}\right) \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}.\frac{\mathrm{sin}\:\mathrm{0}}{\mathrm{cos}\:\mathrm{0}+\mathrm{1}}\right)=−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{0}}{\mathrm{1}+\mathrm{1}}\right)=\mathrm{0} \\ $$$$ \\ $$
Commented by aliyn last updated on 05/Oct/21
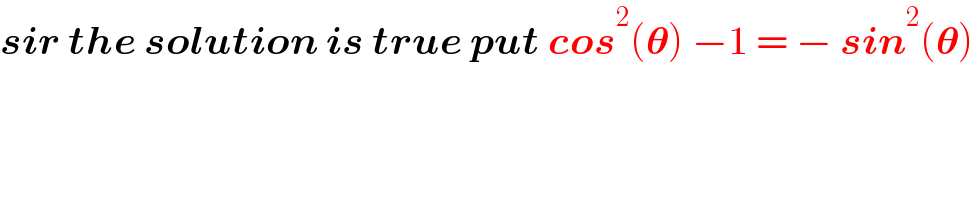
sir the solution is true put cos^2 (𝛉) −1 = − sin^2 (𝛉)
$$\boldsymbol{{sir}}\:\boldsymbol{{the}}\:\boldsymbol{{solution}}\:\boldsymbol{{is}}\:\boldsymbol{{true}}\:\boldsymbol{{put}}\:\boldsymbol{{cos}}^{\mathrm{2}} \left(\boldsymbol{\theta}\right)\:−\mathrm{1}\:=\:−\:\boldsymbol{{sin}}^{\mathrm{2}} \left(\boldsymbol{\theta}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 05/Oct/21
Thank you sir!Now I′ve corrected.
$$\mathcal{T}{hank}\:{you}\:{sir}!{Now}\:{I}'{ve}\:{corrected}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *