Question Number 147101 by mathmax by abdo last updated on 18/Jul/21
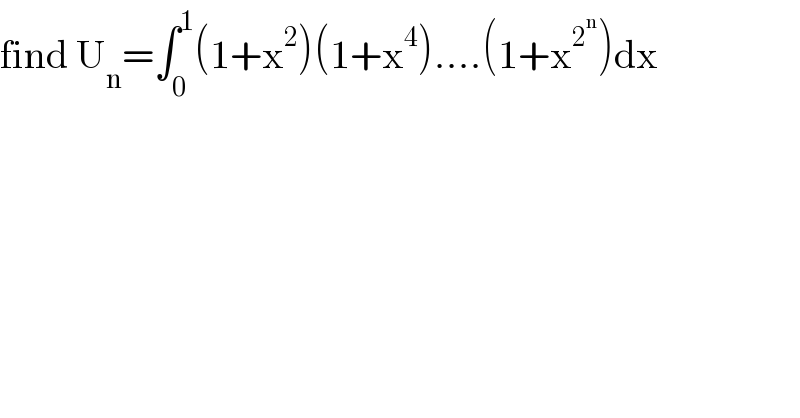
$$\mathrm{find}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)….\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}^{\mathrm{n}} } \right)\mathrm{dx} \\ $$
Answered by gsk2684 last updated on 18/Jul/21
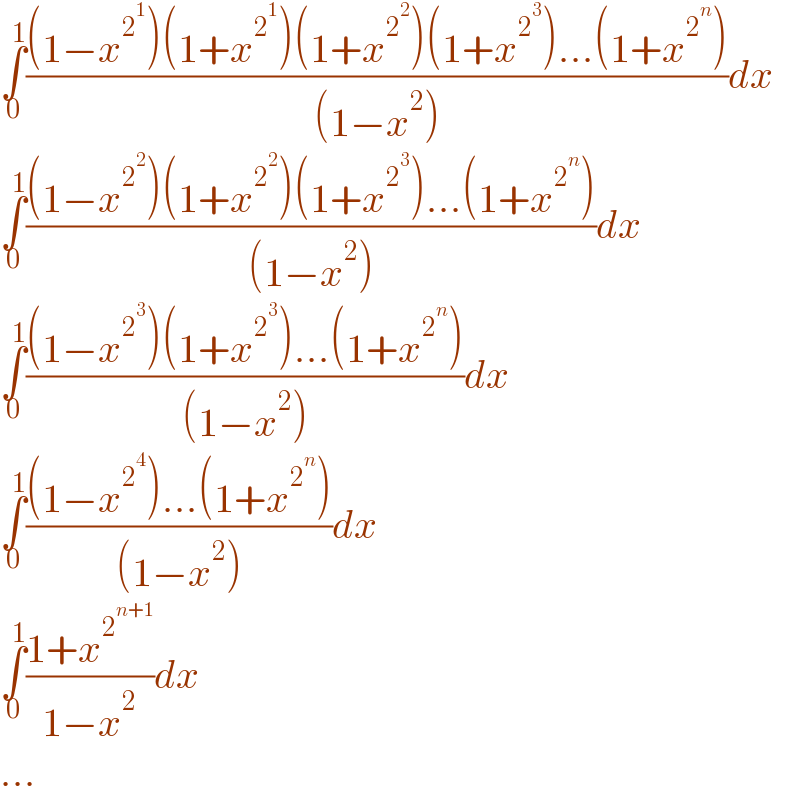
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\left(\mathrm{1}−{x}^{\mathrm{2}^{\mathrm{1}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{1}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{2}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{3}} } \right)…\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{dx} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\left(\mathrm{1}−{x}^{\mathrm{2}^{\mathrm{2}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{2}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{3}} } \right)…\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{dx}\:\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\left(\mathrm{1}−{x}^{\mathrm{2}^{\mathrm{3}} } \right)\left(\mathrm{1}+{x}^{\mathrm{2}^{\mathrm{3}} } \right)…\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{dx}\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\left(\mathrm{1}−{x}^{\mathrm{2}^{\mathrm{4}} } \right)…\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right)}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{dx} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}+{x}^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$… \\ $$
