Question Number 124919 by mathmax by abdo last updated on 07/Dec/20
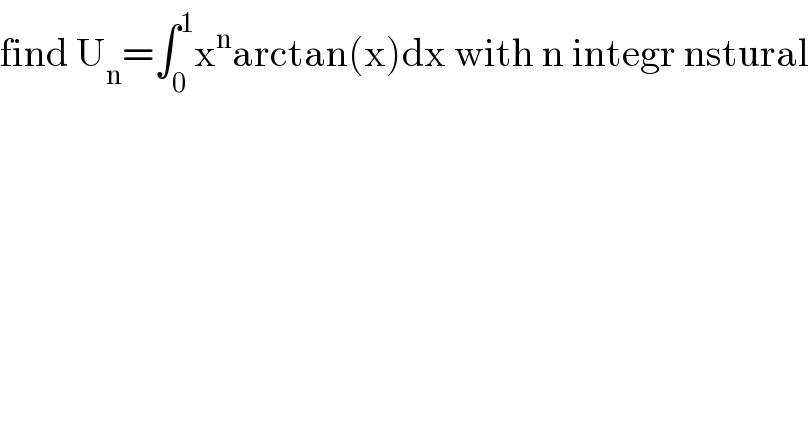
$$\mathrm{find}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}} \mathrm{arctan}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{with}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{nstural} \\ $$
Commented by mindispower last updated on 07/Dec/20
![by part=[(x^(n+1) /(n+1))tan^(−1) (x)]_0 ^1 −(1/(n+1))∫_0 ^1 (x^(n+1) /(1+x^2 ))dx =(π/(4(n+1)))−(1/(n+1))∫_0 ^1 Σ_(k≥0) (−1)^k x^(n+1+2k) dx =(π/(4(n+1)))−(1/((n+1)))Σ_(k≥0) (((−1)^k )/(n+2+2k)) =(π/(4(n+1)))−(1/(n+1))Σ_(k≥0) (((n+2+2(2k+1))−(n+2+4k))/((n+2+2.2k)(n+2+2(2k+1))) =(π/(4(n+1)))−(1/(n+1))Σ_(k≥1) (2/((n−2+4k)(n+4k))) =(π/(4(n+1)))−(1/(8(n+1)))Σ_(k≥1) (1/((((n−1)/4)+k)((n/4)+k))) =(π/(4(n+1)))−(1/(8(n+1))).((Ψ((n/4))−Ψ(((n−1)/4)))/((n/4)−((n−1)/4))) =(π/(4(n+1)))−(1/(2(n+1)))(Ψ((n/4))−Ψ(((n−1)/4))),n≥1 n=0 we get (π/4)−∫_0 ^1 (x/(1+x^2 ))=(π/4)−ln((√2))](https://www.tinkutara.com/question/Q124950.png)
$${by}\:{part}=\left[\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} {x}^{{n}+\mathrm{1}+\mathrm{2}{k}} {dx} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{n}+\mathrm{2}+\mathrm{2}{k}} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left({n}+\mathrm{2}+\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\right)−\left({n}+\mathrm{2}+\mathrm{4}{k}\right)}{\left({n}+\mathrm{2}+\mathrm{2}.\mathrm{2}{k}\right)\left({n}+\mathrm{2}+\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\right.} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}}{\left({n}−\mathrm{2}+\mathrm{4}{k}\right)\left({n}+\mathrm{4}{k}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{8}\left({n}+\mathrm{1}\right)}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\frac{{n}−\mathrm{1}}{\mathrm{4}}+{k}\right)\left(\frac{{n}}{\mathrm{4}}+{k}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{8}\left({n}+\mathrm{1}\right)}.\frac{\Psi\left(\frac{{n}}{\mathrm{4}}\right)−\Psi\left(\frac{{n}−\mathrm{1}}{\mathrm{4}}\right)}{\frac{{n}}{\mathrm{4}}−\frac{{n}−\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\pi}{\mathrm{4}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left(\Psi\left(\frac{{n}}{\mathrm{4}}\right)−\Psi\left(\frac{{n}−\mathrm{1}}{\mathrm{4}}\right)\right),{n}\geqslant\mathrm{1} \\ $$$${n}=\mathrm{0} \\ $$$${we}\:{get}\:\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Bird last updated on 07/Dec/20

$${thanks}\:{sir} \\ $$
