Menu Close

find-u-n-0-sin-n-x-x-dx-n-1-

Tinku Tara 0 Comments
Pin




Question Number 116533 by Bird last updated on 04/Oct/20
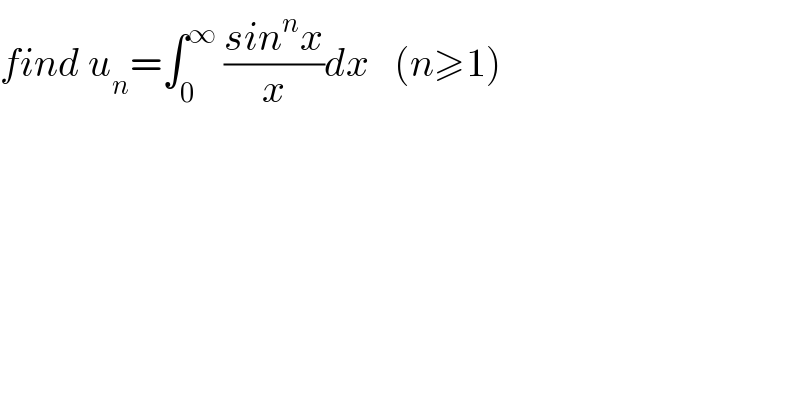
find u_n =∫_0 ^∞ ((sin^n x)/x)dx (n≥1)
$${find}\:{u}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{{n}} {x}}{{x}}{dx}\:\:\:\left({n}\geqslant\mathrm{1}\right) \\ $$
Answered by Olaf last updated on 04/Oct/20
1st case : n is odd sin^n x = (1/2^(n−1) )(−1)^((n−1)/2) Σ_(k=0) ^((n−1)/2) (−1)^k C_n ^k sin[(n−2k)x] u_n = (1/2^(n−1) )(−1)^((n−1)/2) Σ_(k=0) ^((n−1)/2) (−1)^k C_n ^k ∫_0 ^∞ ((sin[(n−2k)x])/x)dx t = (n−2k)x u_n = (1/2^(n−1) )(−1)^((n−1)/2) Σ_(k=0) ^((n−1)/2) (−1)^k C_n ^k ∫_0 ^∞ ((sint)/t)dt With ∫_0 ^∞ ((sint)/t)dt = (π/2) (Dirichlet) u_n = (π/2^n )(−1)^((n−1)/2) Σ_(k=0) ^((n−1)/2) (−1)^k C_n ^k 2nd case : n is even sin^n x = (1/2^(n−1) )(−1)^(n/2) (Σ_(k=0) ^((n−2)/2) (−1)^k C_n ^k cos[(n−2k)x]+(1/2)(−1)^(n/2) C_n ^(n/2) ) u_n = (1/2^(n−1) )(−1)^(n/2) (Σ_(k=0) ^((n−2)/2) (−1)^k C_n ^k ∫_0 ^∞ ((cos[(n−2k)x])/x)dx+(1/2)(−1)^(n/2) C_n ^(n/2) ∫_0 ^∞ (dx/x)) u_n = (1/2^(n−1) )(−1)^(n/2) (Σ_(k=0) ^((n−2)/2) (−1)^k C_n ^k ∫_0 ^∞ ((cost)/t)dt+(1/2)(−1)^(n/2) C_n ^(n/2) ∫_0 ^∞ (dt/t)) ????
$$\mathrm{1st}\:\mathrm{case}\::\:{n}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\mathrm{sin}^{{n}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{1}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \mathrm{sin}\left[\left({n}−\mathrm{2}{k}\right){x}\right] \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{1}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left[\left({n}−\mathrm{2}{k}\right){x}\right]}{{x}}{dx} \\ $$$${t}\:=\:\left({n}−\mathrm{2}{k}\right){x} \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{1}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{t}}{dt} \\ $$$$\mathrm{With}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{t}}{{t}}{dt}\:=\:\frac{\pi}{\mathrm{2}}\:\left(\mathrm{Dirichlet}\right) \\ $$$${u}_{{n}} \:=\:\frac{\pi}{\mathrm{2}^{{n}} }\left(−\mathrm{1}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} \underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{1}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \\ $$$$ \\ $$$$\mathrm{2nd}\:\mathrm{case}\::\:{n}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{sin}^{{n}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} \left(\underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{2}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \mathrm{cos}\left[\left({n}−\mathrm{2}{k}\right){x}\right]+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} {C}_{{n}} ^{\frac{{n}}{\mathrm{2}}} \right) \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} \left(\underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{2}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\left[\left({n}−\mathrm{2}{k}\right){x}\right]}{{x}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} {C}_{{n}} ^{\frac{{n}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}}\right) \\ $$$${u}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} \left(\underset{{k}=\mathrm{0}} {\overset{\frac{{n}−\mathrm{2}}{\mathrm{2}}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}{t}}{{t}}{dt}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\frac{{n}}{\mathrm{2}}} {C}_{{n}} ^{\frac{{n}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \frac{{dt}}{{t}}\right) \\ $$$$???? \\ $$
Commented by mathmax by abdo last updated on 04/Oct/20
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maths mind last updated on 04/Oct/20
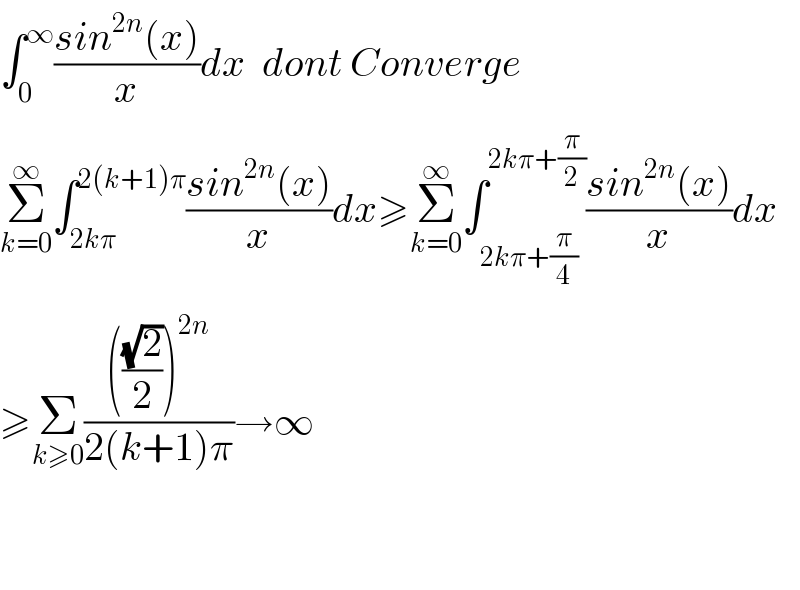
∫_0 ^∞ ((sin^(2n) (x))/x)dx dont Converge Σ_(k=0) ^∞ ∫_(2kπ) ^(2(k+1)π) ((sin^(2n) (x))/x)dx≥Σ_(k=0) ^∞ ∫_(2kπ+(π/4)) ^(2kπ+(π/2)) ((sin^(2n) (x))/x)dx ≥Σ_(k≥0) (((((√2)/2))^(2n) )/(2(k+1)π))→∞
$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}{n}} \left({x}\right)}{{x}}{dx}\:\:{dont}\:{Converge} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{2}{k}\pi} ^{\mathrm{2}\left({k}+\mathrm{1}\right)\pi} \frac{{sin}^{\mathrm{2}{n}} \left({x}\right)}{{x}}{dx}\geqslant\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}} ^{\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}{n}} \left({x}\right)}{{x}}{dx} \\ $$$$\geqslant\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}{n}} }{\mathrm{2}\left({k}+\mathrm{1}\right)\pi}\rightarrow\infty \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 04/Oct/20
we have sinx =((e^(ix) −e^(−ix) )/(2i)) ⇒sin^n x =(1/((2i)^n ))(e^(ix) −e^(−ix) )^n =(1/((2i)^n ))Σ_(k=0) ^n C_(n ) ^k (e^(ix) )^k (−e^(−ix) )^(n−k) =(1/((2i)^n )) Σ_(k=0) ^n C_n ^k e^(ikx) (−1)^(n−k) e^(−i(n−k)x) =(1/((2i)^n )) Σ_(k.0) ^n (−1)^k C_n ^k e^(ikx−(n−k)ix) =(1/((2i)^n )) Σ_(k=0) ^n (−1)^k C_n ^k e^(i(2k−n)x) =(1/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k {cos(2k−n)x +isin(2k−n)x} ⇒ u_n =(1/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx +(i/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((sin(2k−n)x)/x)dx ∫_0 ^∞ ((sin(2k−n)x)/x)dx =_(2k−n)x=t) (2k−n) ∫_0 ^∞ ((sint)/t)(dt/(2k−n)) =(π/2) ⇒ u_n =(1/((2i)^n )) Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx+(π/2)(i/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ∫_0 ^∞ ((cos(2k−n)x)/x)dx =_((2k−n)x=t) (2k−n) ∫_0 ^∞ ((cost)/t)(dt/(2k−n)) =∫_0 ^∞ ((cost)/t) dt =Re(∫_0 ^∞ (e^(it) /t)dt) but ∫_0 ^∞ (e^(it) /t) dt =∫_0 ^∞ (e^(−(−it)) /t)dt =_(−it =u) ∫_0 ^(i∞) (e^(−u) /(u/(−i)))idu =∫_0 ^(i∞) u^(−1) e^(−u) du ....be continued....
$$\mathrm{we}\:\mathrm{have}\:\:\mathrm{sinx}\:=\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}\:\Rightarrow\mathrm{sin}^{\mathrm{n}} \mathrm{x}\:=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\left(\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}\:} ^{\mathrm{k}} \:\:\:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(−\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{n}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{i}\left(\mathrm{n}−\mathrm{k}\right)\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}.\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}−\left(\mathrm{n}−\mathrm{k}\right)\mathrm{ix}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left\{\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\:+\mathrm{isin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}\right\}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}}{\mathrm{x}}\mathrm{dx}\:+\frac{\mathrm{i}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{sin}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}}{\mathrm{x}}\mathrm{dx}\:=_{\left.\mathrm{2k}−\mathrm{n}\right)\mathrm{x}=\mathrm{t}} \:\:\left(\mathrm{2k}−\mathrm{n}\right)\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{2k}−\mathrm{n}} \\ $$$$=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}}{\mathrm{x}}\mathrm{dx}+\frac{\pi}{\mathrm{2}}\frac{\mathrm{i}}{\left(\mathrm{2i}\right)^{\mathrm{n}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}}{\mathrm{x}}\mathrm{dx}\:\:=_{\left(\mathrm{2k}−\mathrm{n}\right)\mathrm{x}=\mathrm{t}} \left(\mathrm{2k}−\mathrm{n}\right)\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cost}}{\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{2k}−\mathrm{n}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cost}}{\mathrm{t}}\:\mathrm{dt}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{it}} }{\mathrm{t}}\mathrm{dt}\right)\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{it}} }{\mathrm{t}}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\left(−\mathrm{it}\right)} }{\mathrm{t}}\mathrm{dt}\:=_{−\mathrm{it}\:=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\mathrm{i}\infty} \:\:\frac{\mathrm{e}^{−\mathrm{u}} }{\frac{\mathrm{u}}{−\mathrm{i}}}\mathrm{idu}\:=\int_{\mathrm{0}} ^{\mathrm{i}\infty} \:\mathrm{u}^{−\mathrm{1}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *