Question Number 81434 by abdomathmax last updated on 13/Feb/20
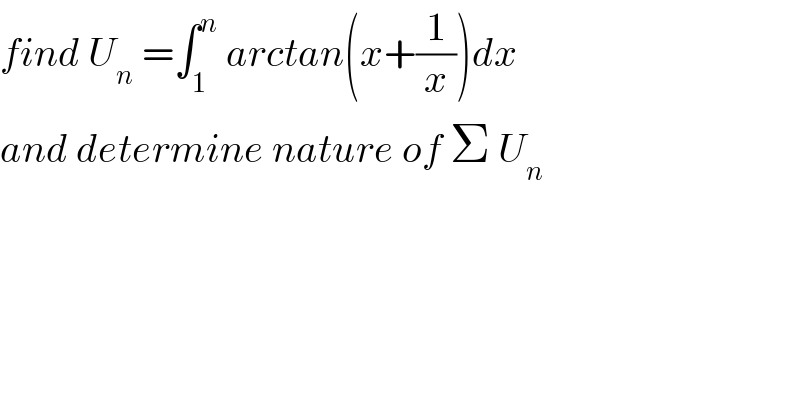
$${find}\:{U}_{{n}} \:=\int_{\mathrm{1}} ^{{n}} \:{arctan}\left({x}+\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$${and}\:{determine}\:{nature}\:{of}\:\Sigma\:{U}_{{n}} \\ $$
Commented by abdomathmax last updated on 13/Feb/20
![by parts U_n =[xarctan(x+(1/x))]_1 ^n −∫_1 ^n x×((1−(1/x^2 ))/(1+(x+(1/x))^2 ))dx =n arctan(n+(1/n))−arctan(2)−∫_1 ^n x×((x^2 −1)/(x^2 {1+(((x^2 +1)^2 )/x^2 )}))dx =narctan(n+(1/n))−arctan(2)−∫_1 ^n ((x^3 −x)/(x^2 +(x^2 +1)^2 ))dx =narctan(n+(1/n))−arctan(2)−∫_1 ^n ((x^3 −x)/(x^2 +x^4 +2x^2 +1))dx =narctan(n+(1/n))−arctan(2)−∫_1 ^n ((x^3 −x)/(x^4 +3x^2 +1))dx x^4 +3x^2 +1=0 →u^2 +3u +1=0(u=x^2 ) ⇒ Δ=9−4=5 ⇒u_1 =((−3+(√5))/2) and u_2 =((−3−(√5))/2) ⇒F(x)=((x^3 −x)/(x^4 +3x^2 +1)) =((x^3 −x)/((x^2 −u_1 )(x^2 −u_2 ))) =((x^3 −x)/(u_1 −u_2 ))((1/(x^2 −u_1 ))−(1/(x^2 −u_2 ))) ⇒ ∫_1 ^n F(x)dx =(1/( (√5)))∫_1 ^n ((x^3 −x)/(x^2 −u_1 ))dx−(1/( (√5))) ∫_1 ^n ((x^3 −x)/(x^2 −u_2 ))dx wehavd ∫_1 ^n ((x^3 −x)/(x^2 −u_1 ))dx =∫_1 ^n ((x(x^2 −u_1 )+xu_1 −x)/(x^2 −u_1 ))dx =(x^2 /2)]_1 ^n +∫_1 ^n (((u_1 −1)x)/(x^2 −u_1 ))dx=(x^2 /2) +((u_1 −1)/2)ln∣x^2 −u_1 ∣ =(n^2 /2)−(1/2) +((u_1 −1)/2)[ln∣x^2 −u_1 ∣]_1 ^n =((n^2 −1)/2) +((u_1 −1)/2){ln(n^2 −u_1 )−ln∣1−u_1 ∣}also we have ∫_1 ^n =((n^2 −1)/2)+((u_2 −1)/2){ln(n^2 −u_2 )−ln∣1−u_2 )} ⇒ U_n =narctan(1+(1/n))−arctan2 −(1/( (√5))){((u_1 −1)/2)ln(n^2 −u_1 )−((u_2 −1)/2)ln(n^2 −u_2 ) +((u_2 −1)/2)ln∣1−u_2 ∣−((u_1 −1)/2)ln∣1−u_1 ∣}](https://www.tinkutara.com/question/Q81508.png)
$${by}\:{parts}\:{U}_{{n}} =\left[{xarctan}\left({x}+\frac{\mathrm{1}}{{x}}\right)\right]_{\mathrm{1}} ^{{n}} −\int_{\mathrm{1}} ^{{n}} {x}×\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{dx} \\ $$$$={n}\:{arctan}\left({n}+\frac{\mathrm{1}}{{n}}\right)−{arctan}\left(\mathrm{2}\right)−\int_{\mathrm{1}} ^{{n}} {x}×\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \left\{\mathrm{1}+\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right\}}{dx} \\ $$$$={narctan}\left({n}+\frac{\mathrm{1}}{{n}}\right)−{arctan}\left(\mathrm{2}\right)−\int_{\mathrm{1}} ^{{n}} \:\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{2}} \:+\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$={narctan}\left({n}+\frac{\mathrm{1}}{{n}}\right)−{arctan}\left(\mathrm{2}\right)−\int_{\mathrm{1}} ^{{n}} \:\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{2}} +{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$={narctan}\left({n}+\frac{\mathrm{1}}{{n}}\right)−{arctan}\left(\mathrm{2}\right)−\int_{\mathrm{1}} ^{{n}} \:\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{4}} \:+\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$${x}^{\mathrm{4}} \:+\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\:\rightarrow{u}^{\mathrm{2}} \:+\mathrm{3}{u}\:+\mathrm{1}=\mathrm{0}\left({u}={x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\Delta=\mathrm{9}−\mathrm{4}=\mathrm{5}\:\Rightarrow{u}_{\mathrm{1}} =\frac{−\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:{and}\:{u}_{\mathrm{2}} =\frac{−\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{4}} \:+\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{{x}^{\mathrm{3}} −{x}}{\left({x}^{\mathrm{2}} −{u}_{\mathrm{1}} \right)\left({x}^{\mathrm{2}} −{u}_{\mathrm{2}} \right)} \\ $$$$=\frac{{x}^{\mathrm{3}} −{x}}{{u}_{\mathrm{1}} −{u}_{\mathrm{2}} }\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{u}_{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{{n}} \:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\int_{\mathrm{1}} ^{{n}} \:\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{2}} −{u}_{\mathrm{1}} }{dx}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\int_{\mathrm{1}} ^{{n}} \frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{2}} −{u}_{\mathrm{2}} }{dx}\:{wehavd} \\ $$$$\int_{\mathrm{1}} ^{{n}} \:\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{2}} −{u}_{\mathrm{1}} }{dx}\:=\int_{\mathrm{1}} ^{{n}} \frac{{x}\left({x}^{\mathrm{2}} −{u}_{\mathrm{1}} \right)+{xu}_{\mathrm{1}} −{x}}{{x}^{\mathrm{2}} −{u}_{\mathrm{1}} }{dx} \\ $$$$\left.=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}} ^{{n}} \:+\int_{\mathrm{1}} ^{{n}} \frac{\left({u}_{\mathrm{1}} −\mathrm{1}\right){x}}{{x}^{\mathrm{2}} −{u}_{\mathrm{1}} }{dx}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{u}_{\mathrm{1}} \mid \\ $$$$=\frac{{n}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{x}^{\mathrm{2}} −{u}_{\mathrm{1}} \mid\right]_{\mathrm{1}} ^{{n}} \\ $$$$=\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\:+\frac{{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{2}}\left\{{ln}\left({n}^{\mathrm{2}} −{u}_{\mathrm{1}} \right)−{ln}\mid\mathrm{1}−{u}_{\mathrm{1}} \mid\right\}{also} \\ $$$${we}\:{have}\: \\ $$$$\left.\int_{\mathrm{1}} ^{{n}} =\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}+\frac{{u}_{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\left\{{ln}\left({n}^{\mathrm{2}} −{u}_{\mathrm{2}} \right)−{ln}\mid\mathrm{1}−{u}_{\mathrm{2}} \right)\right\}\:\Rightarrow \\ $$$${U}_{{n}} ={narctan}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)−{arctan}\mathrm{2} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left\{\frac{{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{2}}{ln}\left({n}^{\mathrm{2}} −{u}_{\mathrm{1}} \right)−\frac{{u}_{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}{ln}\left({n}^{\mathrm{2}} −{u}_{\mathrm{2}} \right)\right. \\ $$$$\left.+\frac{{u}_{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{u}_{\mathrm{2}} \mid−\frac{{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{u}_{\mathrm{1}} \mid\right\} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 13/Feb/20
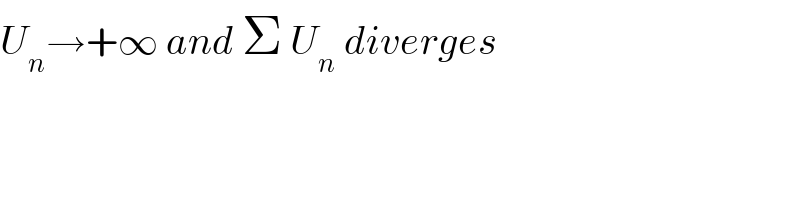
$${U}_{{n}} \rightarrow+\infty\:{and}\:\Sigma\:{U}_{{n}} \:{diverges} \\ $$
Answered by mind is power last updated on 13/Feb/20
![U_n ≥∫_1 ^n arvtan(x)dx ⇒Un≥[xarctan(x)−((ln(1+x^2 ))/2)]_1 ^n U_n ≥narctan(n)−((ln(1+n^2 ))/2)−(π/4)+((ln(2))/2) narctan(n)−((ln(1+n^2 ))/2)=n(arctan(n)−((ln(1+n^2 ))/(2n)))+((ln(2))/2)−(π/4)→∞ ⇒ΣU_n diverge](https://www.tinkutara.com/question/Q81476.png)
$${U}_{{n}} \geqslant\int_{\mathrm{1}} ^{{n}} {arvtan}\left({x}\right){dx} \\ $$$$\Rightarrow{Un}\geqslant\left[{xarctan}\left({x}\right)−\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{2}}\right]_{\mathrm{1}} ^{{n}} \\ $$$${U}_{{n}} \geqslant{narctan}\left({n}\right)−\frac{{ln}\left(\mathrm{1}+{n}^{\mathrm{2}} \right)}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${narctan}\left({n}\right)−\frac{{ln}\left(\mathrm{1}+{n}^{\mathrm{2}} \right)}{\mathrm{2}}={n}\left({arctan}\left({n}\right)−\frac{{ln}\left(\mathrm{1}+{n}^{\mathrm{2}} \right)}{\mathrm{2}{n}}\right)+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\rightarrow\infty \\ $$$$\Rightarrow\Sigma{U}_{{n}} \:{diverge} \\ $$
