Question Number 178282 by Sheshdevsahu last updated on 14/Oct/22
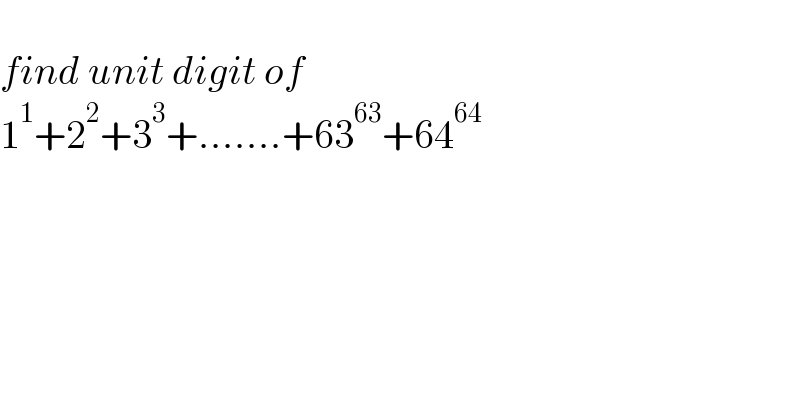
$$ \\ $$$${find}\:{unit}\:{digit}\:{of}\: \\ $$$$\mathrm{1}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +…….+\mathrm{63}^{\mathrm{63}} +\mathrm{64}^{\mathrm{64}} \\ $$
Answered by mr W last updated on 14/Oct/22

$$\left(…\mathrm{0}\right)^{{n}} =…\mathrm{0} \\ $$$$\mathrm{10}^{\mathrm{10}} +\mathrm{20}^{\mathrm{20}} +\mathrm{30}^{\mathrm{30}} +\mathrm{40}^{\mathrm{49}} +\mathrm{50}^{\mathrm{50}} +\mathrm{60}^{\mathrm{60}} =…\mathrm{0} \\ $$$$\left(…\mathrm{1}\right)^{{n}} =…\mathrm{1} \\ $$$$\mathrm{1}^{\mathrm{1}} +\mathrm{11}^{\mathrm{11}} +\mathrm{21}^{\mathrm{21}} +\mathrm{31}^{\mathrm{31}} +\mathrm{41}^{\mathrm{41}} +\mathrm{51}^{\mathrm{51}} +\mathrm{61}^{\mathrm{61}} =…\mathrm{1}×\mathrm{7}=…\mathrm{7} \\ $$$$\left(…\mathrm{5}\right)^{{n}} =…\mathrm{5} \\ $$$$\mathrm{5}^{\mathrm{5}} +\mathrm{15}^{\mathrm{15}} +\mathrm{25}^{\mathrm{25}} +\mathrm{35}^{\mathrm{35}} +\mathrm{45}^{\mathrm{45}} +\mathrm{55}^{\mathrm{55}} =…\mathrm{5}×\mathrm{6}=…\mathrm{0} \\ $$$$\left(…\mathrm{6}\right)^{{n}} =…\mathrm{6} \\ $$$$\mathrm{6}^{\mathrm{6}} +\mathrm{16}^{\mathrm{16}} +\mathrm{26}^{\mathrm{26}} +\mathrm{36}^{\mathrm{36}} +\mathrm{46}^{\mathrm{46}} +\mathrm{56}^{\mathrm{56}} =…\mathrm{6}×\mathrm{6}=…\mathrm{6} \\ $$$$\left(…\mathrm{2}\right)^{\mathrm{4}{n}+\mathrm{1}/\mathrm{2}/\mathrm{3}/\mathrm{4}} =…\mathrm{2}/\mathrm{4}/\mathrm{8}/\mathrm{6} \\ $$$$\mathrm{2}^{\mathrm{2}} +\mathrm{12}^{\mathrm{12}} +\mathrm{22}^{\mathrm{22}} +\mathrm{32}^{\mathrm{32}} +\mathrm{42}^{\mathrm{42}} +\mathrm{52}^{\mathrm{52}} +\mathrm{62}^{\mathrm{62}} =…\mathrm{4}+\mathrm{6}+\mathrm{4}+\mathrm{6}+\mathrm{4}+\mathrm{6}+\mathrm{4}=…\mathrm{4} \\ $$$$\left(…\mathrm{3}\right)^{\mathrm{4}{n}+\mathrm{1}/\mathrm{2}/\mathrm{3}/\mathrm{4}} =…\mathrm{3}/\mathrm{9}/\mathrm{7}/\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{3}} +\mathrm{13}^{\mathrm{13}} +\mathrm{23}^{\mathrm{23}} +\mathrm{33}^{\mathrm{33}} +\mathrm{43}^{\mathrm{43}} +\mathrm{53}^{\mathrm{53}} +\mathrm{63}^{\mathrm{63}} =…\mathrm{7}+\mathrm{3}+\mathrm{7}+\mathrm{3}+\mathrm{7}+\mathrm{3}+\mathrm{7}=…\mathrm{7} \\ $$$$\left(…\mathrm{4}\right)^{\mathrm{2}{n}+\mathrm{1}/\mathrm{2}} =…\mathrm{4}/\mathrm{6} \\ $$$$\mathrm{4}^{\mathrm{4}} +\mathrm{14}^{\mathrm{14}} +\mathrm{24}^{\mathrm{24}} +\mathrm{34}^{\mathrm{34}} +\mathrm{44}^{\mathrm{44}} +\mathrm{54}^{\mathrm{54}} +\mathrm{64}^{\mathrm{64}} =…\mathrm{6}×\mathrm{7}=…\mathrm{2} \\ $$$$\left(…\mathrm{7}\right)^{\mathrm{4}{n}+\mathrm{1}/\mathrm{2}/\mathrm{3}/\mathrm{4}} =…\mathrm{7}/\mathrm{9}/\mathrm{3}/\mathrm{1} \\ $$$$\mathrm{7}^{\mathrm{7}} +\mathrm{17}^{\mathrm{17}} +\mathrm{27}^{\mathrm{27}} +\mathrm{37}^{\mathrm{37}} +\mathrm{47}^{\mathrm{47}} +\mathrm{57}^{\mathrm{57}} =…\mathrm{3}+\mathrm{7}+\mathrm{3}+\mathrm{7}+\mathrm{3}+\mathrm{7}=…\mathrm{0} \\ $$$$\left(…\mathrm{8}\right)^{\mathrm{4}{n}+\mathrm{1}/\mathrm{2}/\mathrm{3}/\mathrm{4}} =…\mathrm{8}/\mathrm{4}/\mathrm{2}/\mathrm{6} \\ $$$$\mathrm{8}^{\mathrm{8}} +\mathrm{18}^{\mathrm{18}} +\mathrm{28}^{\mathrm{28}} +\mathrm{38}^{\mathrm{38}} +\mathrm{48}^{\mathrm{48}} +\mathrm{58}^{\mathrm{58}} =…\mathrm{6}+\mathrm{4}+\mathrm{6}+\mathrm{4}+\mathrm{6}+\mathrm{4}=…\mathrm{0} \\ $$$$\left(…\mathrm{9}\right)^{\mathrm{2}{n}+\mathrm{1}/\mathrm{2}} =…\mathrm{9}/\mathrm{1} \\ $$$$\mathrm{9}^{\mathrm{9}} +\mathrm{19}^{\mathrm{19}} +\mathrm{29}^{\mathrm{29}} +\mathrm{39}^{\mathrm{39}} +\mathrm{49}^{\mathrm{49}} +\mathrm{59}^{\mathrm{59}} =…\mathrm{9}×\mathrm{6}=…\mathrm{4} \\ $$$$ \\ $$$$\mathrm{1}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +…+\mathrm{64}^{\mathrm{64}} =…\mathrm{0}+\mathrm{7}+\mathrm{0}+\mathrm{6}+\mathrm{4}+\mathrm{7}+\mathrm{2}+\mathrm{0}+\mathrm{0}+\mathrm{4}=…\mathrm{0} \\ $$
Commented by mr W last updated on 14/Oct/22
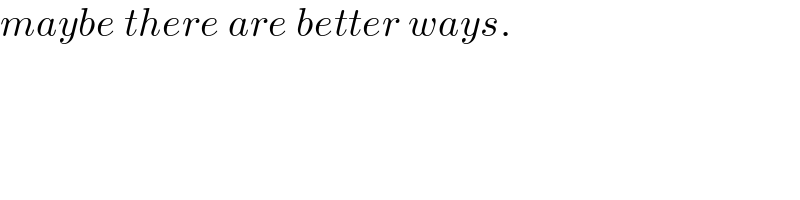
$${maybe}\:{there}\:{are}\:{better}\:{ways}. \\ $$
Commented by Tawa11 last updated on 14/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 14/Oct/22

Answered by mahdipoor last updated on 14/Oct/22
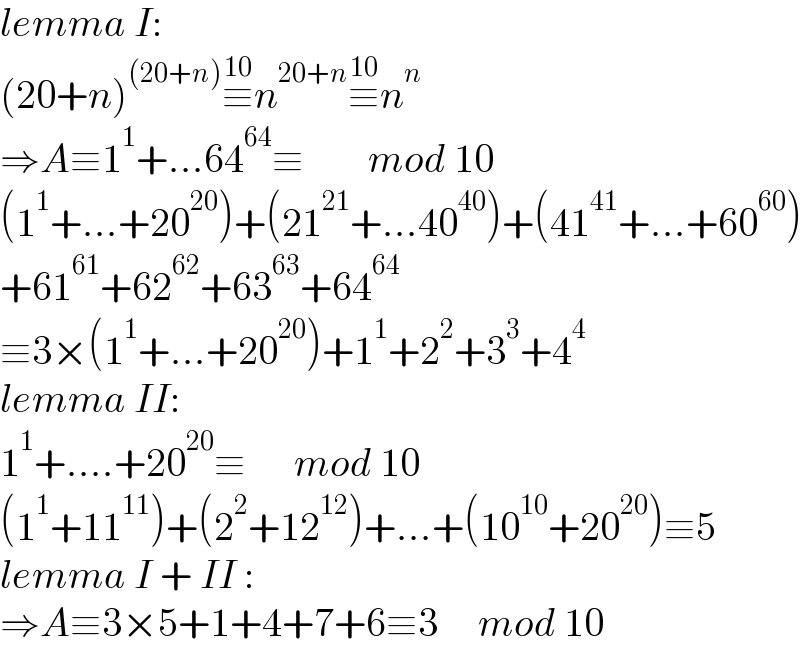
$${lemma}\:{I}: \\ $$$$\left(\mathrm{20}+{n}\right)^{\left(\mathrm{20}+{n}\right)} \overset{\mathrm{10}} {\equiv}{n}^{\mathrm{20}+{n}} \overset{\mathrm{10}} {\equiv}{n}^{{n}} \:\:\: \\ $$$$\Rightarrow{A}\equiv\mathrm{1}^{\mathrm{1}} +…\mathrm{64}^{\mathrm{64}} \equiv\:\:\:\:\:\:\:\:{mod}\:\mathrm{10} \\ $$$$\left(\mathrm{1}^{\mathrm{1}} +…+\mathrm{20}^{\mathrm{20}} \right)+\left(\mathrm{21}^{\mathrm{21}} +…\mathrm{40}^{\mathrm{40}} \right)+\left(\mathrm{41}^{\mathrm{41}} +…+\mathrm{60}^{\mathrm{60}} \right) \\ $$$$+\mathrm{61}^{\mathrm{61}} +\mathrm{62}^{\mathrm{62}} +\mathrm{63}^{\mathrm{63}} +\mathrm{64}^{\mathrm{64}} \\ $$$$\equiv\mathrm{3}×\left(\mathrm{1}^{\mathrm{1}} +…+\mathrm{20}^{\mathrm{20}} \right)+\mathrm{1}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +\mathrm{4}^{\mathrm{4}} \:\:\: \\ $$$${lemma}\:{II}: \\ $$$$\mathrm{1}^{\mathrm{1}} +….+\mathrm{20}^{\mathrm{20}} \equiv\:\:\:\:\:\:{mod}\:\mathrm{10} \\ $$$$\left(\mathrm{1}^{\mathrm{1}} +\mathrm{11}^{\mathrm{11}} \right)+\left(\mathrm{2}^{\mathrm{2}} +\mathrm{12}^{\mathrm{12}} \right)+…+\left(\mathrm{10}^{\mathrm{10}} +\mathrm{20}^{\mathrm{20}} \right)\equiv\mathrm{5} \\ $$$${lemma}\:{I}\:+\:{II}\:: \\ $$$$\Rightarrow{A}\equiv\mathrm{3}×\mathrm{5}+\mathrm{1}+\mathrm{4}+\mathrm{7}+\mathrm{6}\equiv\mathrm{3}\:\:\:\:\:{mod}\:\mathrm{10} \\ $$
