Question Number 79758 by mathmax by abdo last updated on 27/Jan/20
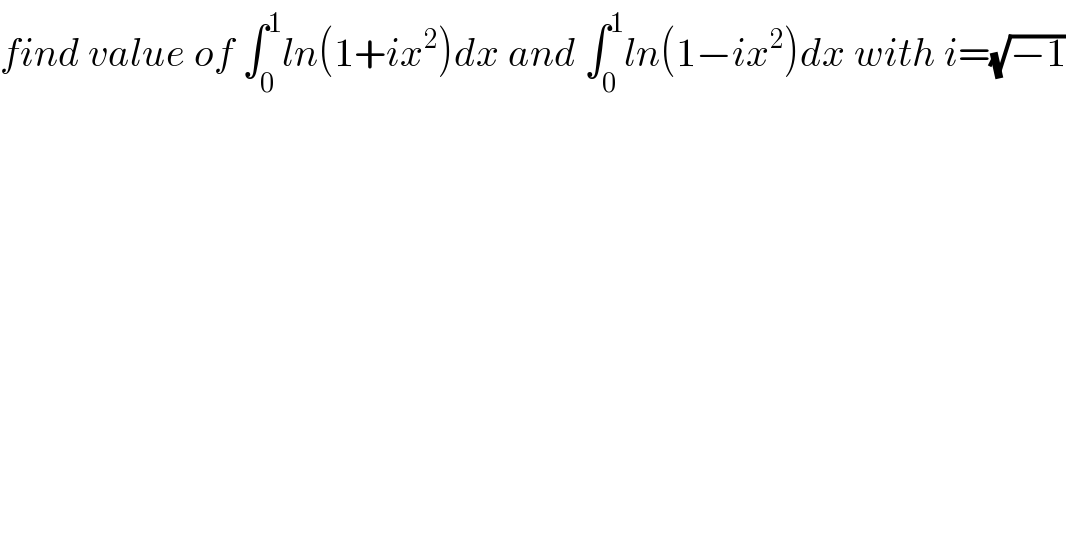
$${find}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}^{\mathrm{2}} \right){dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{ix}^{\mathrm{2}} \right){dx}\:{with}\:{i}=\sqrt{−\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 29/Jan/20
![let z from C and f(z)=∫_0 ^1 ln(1+zx^2 )dx ⇒ f^′ (z)=∫_0 ^1 (x^2 /(1+zx^2 ))dx =(1/z) ∫_0 ^1 ((zx^2 +1−1)/(1+zx^2 ))dx =(1/z) −(1/z) ∫_0 ^1 (dx/(1+zx^2 )) and ∫_0 ^1 (dx/(1+zx^2 )) =_(x(√z)=t) ∫_0 ^(√z) (dt/( (√z)(1+t^2 ))) =(1/( (√z))) arctan((√z)) ⇒f^′ (z)=(1/z)−((arctan((√z)))/(z(√z))) ⇒ f(z)=lnz +∫_1 ^z ((arctan((√u)))/(u(√u))) du +c (u=t^2 ) =lnz +∫_1 ^(√z) ((arctan(t))/t^3 )(2t)dt +c =ln(z)+2∫_1 ^(√z) ((arctan(t))/t^2 )dt +c f(1) =∫_0 ^1 ln(1+x^2 )dx =c ⇒ f(z) =lnz +2∫_1 ^(√z) ((arctan(t))/t^2 )dt +∫_0 ^1 ln(1+x^2 )dx we have by parts ∫_1 ^(√z) ((arctan(t))/t^2 )dt =[−((arctant)/t)]_1 ^(√z) +∫_1 ^(√z) (1/(t(1+t^2 )))dt =(π/4)−((arctan((√z)))/( (√z))) +∫_1 ^(√z) ((1/t)−(t/(t^2 +1)))dt =(π/4)−((arctan((√z)))/( (√z))) +ln((√z))−[(1/2)ln(t^2 +1)]_1 ^(√z) =(π/4)−((arctan((√z)))/( (√z))) +(1/2)ln(z)−(1/2){ln(z+1)−ln(2)} ⇒ f(z)=ln(z)+(π/2)−((2arctan((√z)))/( (√z))) +ln(z)−ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx f(z)=2ln(z)+(π/2) −2((arctan((√z)))/( (√z))) −ln(z+1)+ln(2)+∫_0 ^1 ln(1+x^2 )dx by parts ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 )/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ×(π/4) =ln(2)−2+(π/2) ⇒ f(z) =2ln(z) +2ln(2) +π −2 −2((arctan((√z)))/( (√z))) −ln(z+1) =∫_0 ^1 ln(1+zx^2 )dx ⇒ ∫_0 ^1 ln(1+ix^2 )dx =f(i) =2ln(i)+2ln(2)+π−2−2 ×((arctan((√i)))/( (√i))) −ln(i+1) =2×((iπ)/2) +2ln(2)+π−2 −2 ×((arctan(e^((iπ)/4) ))/e^((iπ)/4) )−ln((√2)e^((iπ)/4) ) =iπ +2ln(2)+π−2 −2e^(−((iπ)/4)) arctan(e^((iπ)/4) )−(1/2)ln(2)−((iπ)/4)](https://www.tinkutara.com/question/Q79889.png)
$${let}\:{z}\:{from}\:{C}\:{and}\:{f}\left({z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{zx}^{\mathrm{2}} \right){dx}\:\Rightarrow \\ $$$${f}^{'} \left({z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{zx}^{\mathrm{2}} }{dx}\:=\frac{\mathrm{1}}{{z}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{zx}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{1}+{zx}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{{z}}\:−\frac{\mathrm{1}}{{z}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{zx}^{\mathrm{2}} }\:{and}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{zx}^{\mathrm{2}} }\:=_{{x}\sqrt{{z}}={t}} \:\:\int_{\mathrm{0}} ^{\sqrt{{z}}} \:\:\:\frac{{dt}}{\:\sqrt{{z}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{z}}}\:{arctan}\left(\sqrt{{z}}\right)\:\Rightarrow{f}^{'} \left({z}\right)=\frac{\mathrm{1}}{{z}}−\frac{{arctan}\left(\sqrt{{z}}\right)}{{z}\sqrt{{z}}}\:\Rightarrow \\ $$$${f}\left({z}\right)={lnz}\:\:+\int_{\mathrm{1}} ^{{z}} \:\frac{{arctan}\left(\sqrt{{u}}\right)}{{u}\sqrt{{u}}}\:{du}\:+{c}\:\:\:\:\left({u}={t}^{\mathrm{2}} \right) \\ $$$$={lnz}\:+\int_{\mathrm{1}} ^{\sqrt{{z}}} \:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{3}} }\left(\mathrm{2}{t}\right){dt}\:+{c}\:={ln}\left({z}\right)+\mathrm{2}\int_{\mathrm{1}} ^{\sqrt{{z}}} \:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:+{c} \\ $$$${f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:={c}\:\Rightarrow \\ $$$${f}\left({z}\right)\:={lnz}\:+\mathrm{2}\int_{\mathrm{1}} ^{\sqrt{{z}}} \:\:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:\:{we}\:{have}\:{by}\:{parts} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{{z}}} \:\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} }{dt}\:=\left[−\frac{{arctant}}{{t}}\right]_{\mathrm{1}} ^{\sqrt{{z}}} +\int_{\mathrm{1}} ^{\sqrt{{z}}} \:\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:+\int_{\mathrm{1}} ^{\sqrt{{z}}} \left(\frac{\mathrm{1}}{{t}}−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt} \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:+{ln}\left(\sqrt{{z}}\right)−\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{1}} ^{\sqrt{{z}}} \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({z}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left({z}+\mathrm{1}\right)−{ln}\left(\mathrm{2}\right)\right\}\:\Rightarrow \\ $$$${f}\left({z}\right)={ln}\left({z}\right)+\frac{\pi}{\mathrm{2}}−\frac{\mathrm{2}{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:+{ln}\left({z}\right)−{ln}\left({z}+\mathrm{1}\right)+{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${f}\left({z}\right)=\mathrm{2}{ln}\left({z}\right)+\frac{\pi}{\mathrm{2}}\:−\mathrm{2}\frac{{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:−{ln}\left({z}+\mathrm{1}\right)+{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${by}\:{parts}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:×\frac{\pi}{\mathrm{4}}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${f}\left({z}\right)\:=\mathrm{2}{ln}\left({z}\right)\:+\mathrm{2}{ln}\left(\mathrm{2}\right)\:+\pi\:−\mathrm{2}\:−\mathrm{2}\frac{{arctan}\left(\sqrt{{z}}\right)}{\:\sqrt{{z}}}\:−{ln}\left({z}+\mathrm{1}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{zx}^{\mathrm{2}} \right){dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}^{\mathrm{2}} \right){dx}\:={f}\left({i}\right)\:=\mathrm{2}{ln}\left({i}\right)+\mathrm{2}{ln}\left(\mathrm{2}\right)+\pi−\mathrm{2}−\mathrm{2}\:×\frac{{arctan}\left(\sqrt{{i}}\right)}{\:\sqrt{{i}}} \\ $$$$−{ln}\left({i}+\mathrm{1}\right) \\ $$$$=\mathrm{2}×\frac{{i}\pi}{\mathrm{2}}\:+\mathrm{2}{ln}\left(\mathrm{2}\right)+\pi−\mathrm{2}\:−\mathrm{2}\:×\frac{{arctan}\left({e}^{\frac{{i}\pi}{\mathrm{4}}} \right)}{{e}^{\frac{{i}\pi}{\mathrm{4}}} }−{ln}\left(\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$$={i}\pi\:+\mathrm{2}{ln}\left(\mathrm{2}\right)+\pi−\mathrm{2}\:−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{arctan}\left({e}^{\frac{{i}\pi}{\mathrm{4}}} \right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{{i}\pi}{\mathrm{4}} \\ $$$$ \\ $$
