find-volume-of-region-in-R-3-given-by-3-x-4-y-3-z-12-is-

Question Number 182368 by universe last updated on 08/Dec/22

find volume of region in R^{3} given by

3 ∣ x ∣ + 4 ∣ y ∣ + 3 ∣ z ∣ ⩽ 12 is

Answered by mr W last updated on 08/Dec/22

\frac{∣ x ∣}{4} + \frac{∣ y ∣}{3} + \frac{∣ z ∣}{4} ⩽ 1

V = 8 \times \frac{4 \times 3 \times 4}{6} = 64

Commented by universe last updated on 09/Dec/22

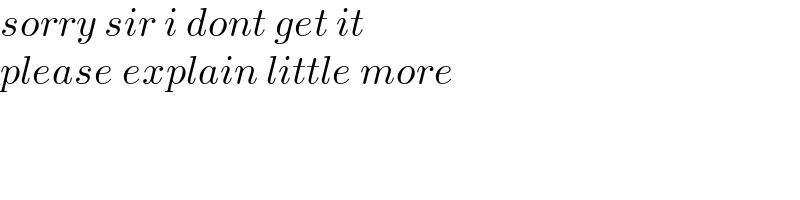
s o r r y s i r i d o n t g e t i t

p l e a s e e x p l a i n l i t t l e m o r e

Commented by mr W last updated on 09/Dec/22

Commented by mr W last updated on 09/Dec/22

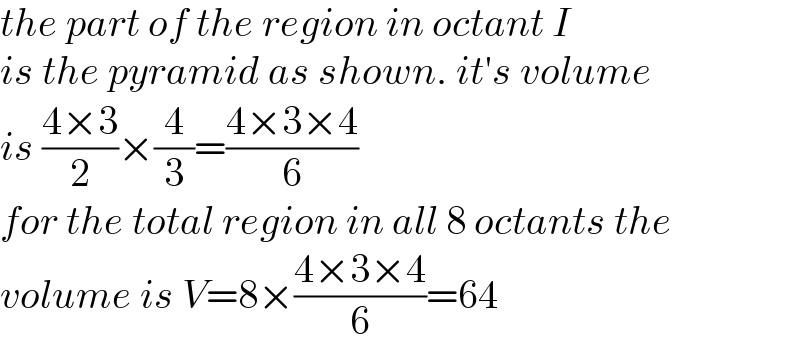
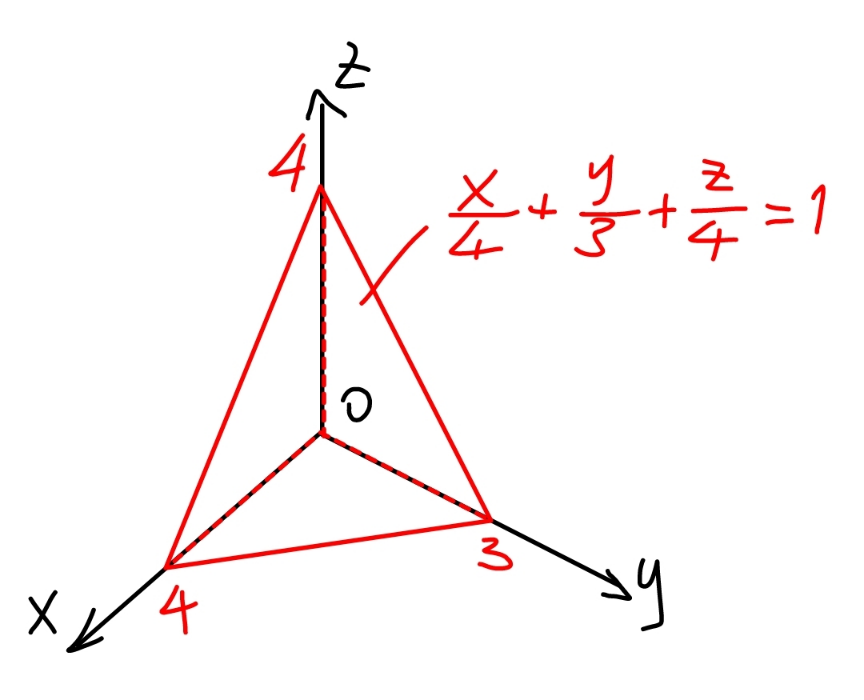
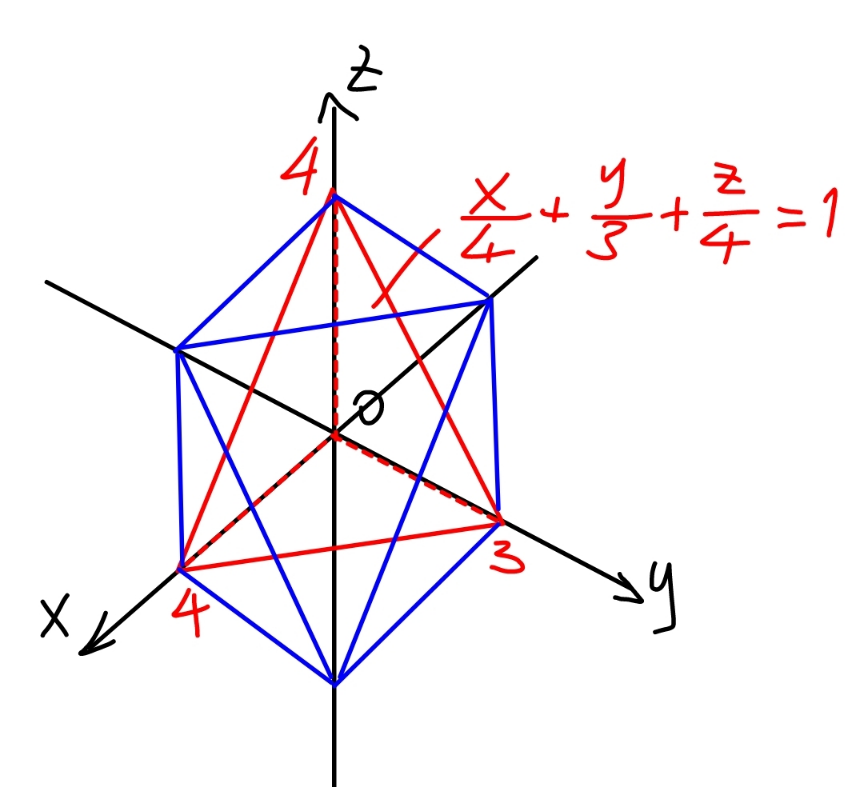
t h e p a r t o f t h e r e g i o n i n o c t a n t I

i s t h e p y r a m i d a s s h o w n . {i t}^{'} s v o l u m e

i s \frac{4 \times 3}{2} \times \frac{4}{3} = \frac{4 \times 3 \times 4}{6}

f o r t h e t o t a l r e g i o n i n a l l 8 o c t a n t s t h e

v o l u m e i s V = 8 \times \frac{4 \times 3 \times 4}{6} = 64

Commented by mr W last updated on 09/Dec/22

Commented by universe last updated on 09/Dec/22

t h a n k s s i r