Question Number 173529 by Shrinava last updated on 13/Jul/22
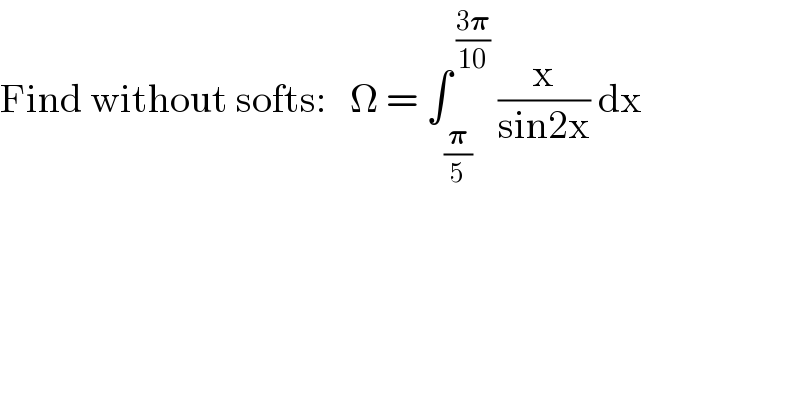
$$\mathrm{Find}\:\mathrm{without}\:\mathrm{softs}:\:\:\:\Omega\:=\:\int_{\frac{\boldsymbol{\pi}}{\mathrm{5}}} ^{\:\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{10}}} \:\frac{\mathrm{x}}{\mathrm{sin2x}}\:\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 13/Jul/22
![I=∫_(π/5) ^((3π)/(10)) (x/(sin2x))dx , x=(π/2)−u ⇒I=∫_(π/5) ^((3π)/(10)) (((π/2)−u)/(sin2u))du=∫_(π/5) ^((3π)/(10)) (((π/2)−x)/(sin2x))dx I+I=2I=∫_(π/5) ^((3π)/(10)) (x/(sin2x))dx+∫_(π/5) ^((3π)/(10)) (((π/2)−x)/(sin2x))dx=(π/2)∫_(π/5) ^((3π)/(10)) (1/(sin2x))dx ⇒I=(π/4)∫_(π/5) ^((3π)/(10)) cosec2xdx=(π/8)ln∣cosec2x−cot2x∣+C =(π/8)ln∣((2sin^2 x)/(2sinxcosx))∣+C=(π/8)[ln(tanx)]_(π/5) ^((3π)/(10))](https://www.tinkutara.com/question/Q173530.png)
$${I}=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{x}}{\mathrm{sin2}{x}}{dx}\:,\:{x}=\frac{\pi}{\mathrm{2}}−{u}\:\Rightarrow{I}=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\frac{\pi}{\mathrm{2}}−{u}}{\mathrm{sin2}{u}}{du}=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\frac{\pi}{\mathrm{2}}−{x}}{\mathrm{sin2}{x}}{dx} \\ $$$${I}+{I}=\mathrm{2}{I}=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{x}}{\mathrm{sin2}{x}}{dx}+\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\frac{\pi}{\mathrm{2}}−{x}}{\mathrm{sin2}{x}}{dx}=\frac{\pi}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\mathrm{1}}{\mathrm{sin2}{x}}{dx} \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{4}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \mathrm{cosec2}{xdx}=\frac{\pi}{\mathrm{8}}\mathrm{ln}\mid\mathrm{cosec2}{x}−\mathrm{cot2}{x}\mid+{C} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{8}}\mathrm{ln}\mid\frac{\mathrm{2sin}^{\mathrm{2}} {x}}{\mathrm{2sin}{x}\mathrm{cos}{x}}\mid+{C}=\frac{\pi}{\mathrm{8}}\left[\mathrm{ln}\left(\mathrm{tan}{x}\right)\right]_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \\ $$
