find-without-using-l-hopital-lim-x-2-e-2-x-1-x-2-4-

Question Number 95832 by M±th+et+s last updated on 28/May/20

$${find}\:{without}\:{using}\:{l}'{hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {{lim}}\frac{{e}^{\mathrm{2}−{x}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{4}} \\ $$

Answered by mathmax by abdo last updated on 28/May/20

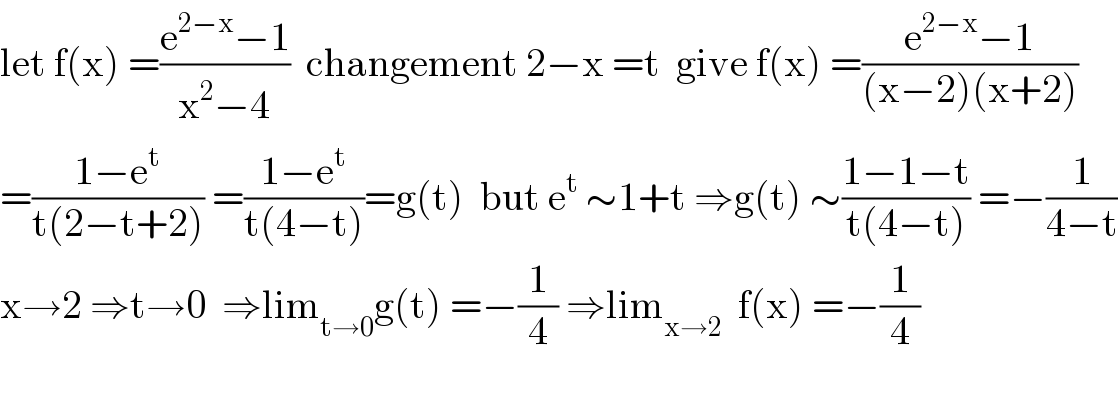
let f(x) =((e^(2−x) −1)/(x^2 −4)) changement 2−x =t give f(x) =((e^(2−x) −1)/((x−2)(x+2))) =((1−e^t )/(t(2−t+2))) =((1−e^t )/(t(4−t)))=g(t) but e^t ∼1+t ⇒g(t) ∼((1−1−t)/(t(4−t))) =−(1/(4−t)) x→2 ⇒t→0 ⇒lim_(t→0) g(t) =−(1/4) ⇒lim_(x→2) f(x) =−(1/4)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}\:\:\mathrm{changement}\:\mathrm{2}−\mathrm{x}\:=\mathrm{t}\:\:\mathrm{give}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\mathrm{2}−\mathrm{x}} −\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}−\mathrm{e}^{\mathrm{t}} }{\mathrm{t}\left(\mathrm{2}−\mathrm{t}+\mathrm{2}\right)}\:=\frac{\mathrm{1}−\mathrm{e}^{\mathrm{t}} }{\mathrm{t}\left(\mathrm{4}−\mathrm{t}\right)}=\mathrm{g}\left(\mathrm{t}\right)\:\:\mathrm{but}\:\mathrm{e}^{\mathrm{t}} \:\sim\mathrm{1}+\mathrm{t}\:\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\:\sim\frac{\mathrm{1}−\mathrm{1}−\mathrm{t}}{\mathrm{t}\left(\mathrm{4}−\mathrm{t}\right)}\:=−\frac{\mathrm{1}}{\mathrm{4}−\mathrm{t}} \\ $$$$\mathrm{x}\rightarrow\mathrm{2}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\:\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}} \:\:\mathrm{f}\left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$

Commented by M±th+et+s last updated on 28/May/20

$${nice}\:{work}\:{thank}\:{you}\:{sir} \\ $$

Commented by mathmax by abdo last updated on 28/May/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$

Answered by Dwaipayan Shikari last updated on 21/Jun/20

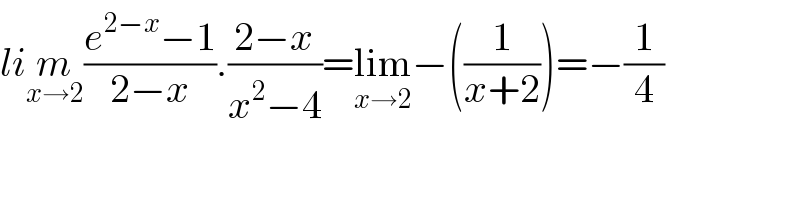
lim_(x→2) ((e^(2−x) −1)/(2−x)).((2−x)/(x^2 −4))=lim_(x→2) −((1/(x+2)))=−(1/4)

$${li}\underset{{x}\rightarrow\mathrm{2}} {{m}}\frac{{e}^{\mathrm{2}−{x}} −\mathrm{1}}{\mathrm{2}−{x}}.\frac{\mathrm{2}−{x}}{{x}^{\mathrm{2}} −\mathrm{4}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}−\left(\frac{\mathrm{1}}{{x}+\mathrm{2}}\right)=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by M±th+et+s last updated on 23/Jun/20

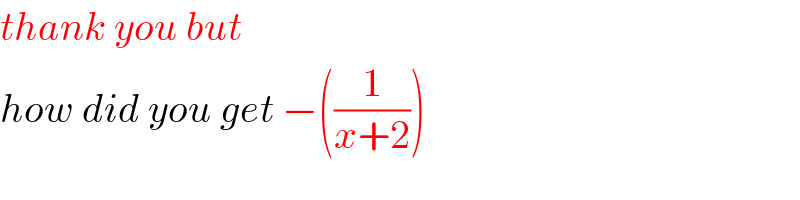
thank you but how did you get −((1/(x+2)))

$${thank}\:{you}\:{but} \\ $$$${how}\:{did}\:{you}\:{get}\:−\left(\frac{\mathrm{1}}{{x}+\mathrm{2}}\right) \\ $$

Commented by Dwaipayan Shikari last updated on 29/Jun/20

$$\frac{{e}^{\mathrm{2}−{x}} −\mathrm{1}}{\mathrm{2}−{x}}=\mathrm{1}\:\: \\ $$

Facebook Tweet Pin

find-without-using-l-hopital-lim-x-2-e-2-x-1-x-2-4-

Leave a Reply Cancel reply