Menu Close

find-x-1-1-x-2-1-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 40620 by math khazana by abdo last updated on 25/Jul/18
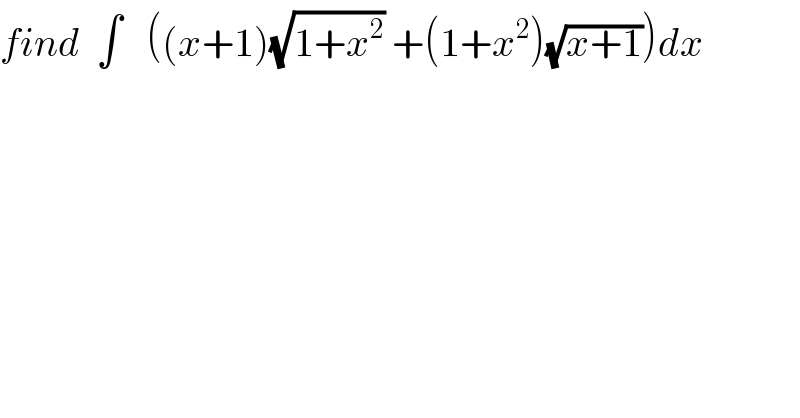
find ∫ ((x+1)(√(1+x^2 )) +(1+x^2 )(√(x+1)))dx
$${find}\:\:\int\:\:\:\left(\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}+\mathrm{1}}\right){dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18
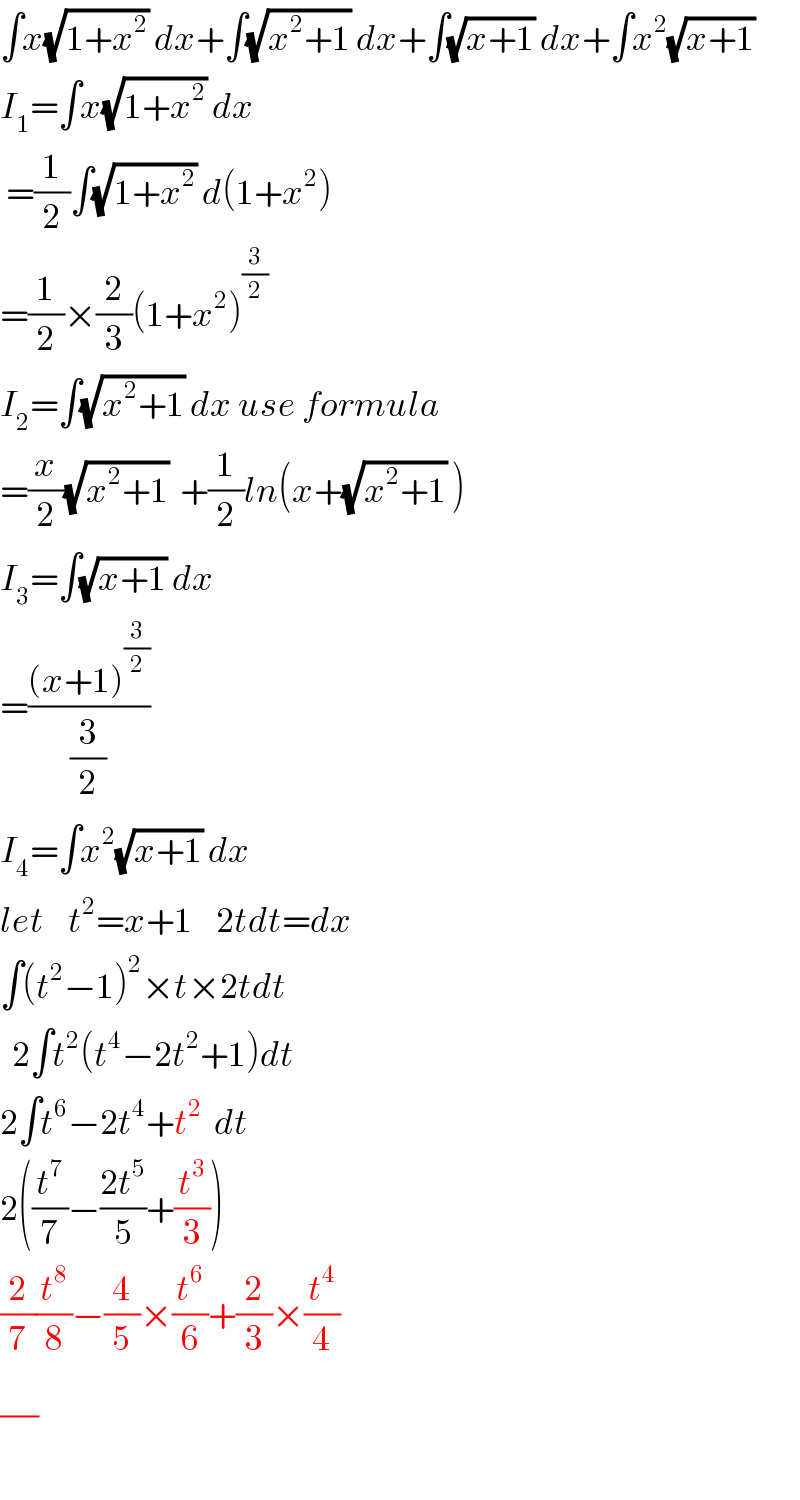
∫x(√(1+x^2 )) dx+∫(√(x^2 +1)) dx+∫(√(x+1)) dx+∫x^2 (√(x+1)) I_1 =∫x(√(1+x^2 )) dx =(1/2)∫(√(1+x^2 )) d(1+x^2 ) =(1/2)×(2/3)(1+x^2 )^(3/2) I_2 =∫(√(x^2 +1)) dx use formula =(x/2)(√(x^2 +1)) +(1/2)ln(x+(√(x^2 +1)) ) I_3 =∫(√(x+1)) dx =(((x+1)^(3/2) )/(3/2)) I_4 =∫x^2 (√(x+1)) dx let t^2 =x+1 2tdt=dx ∫(t^2 −1)^2 ×t×2tdt 2∫t^2 (t^4 −2t^2 +1)dt 2∫t^6 −2t^4 +t^2 dt 2((t^7 /7)−((2t^5 )/5)+(t^3 /3)) (2/7)(t^8 /8)−(4/5)×(t^6 /6)+(2/3)×(t^4 /4) (/)
$$\int{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}+\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}+\int\sqrt{{x}+\mathrm{1}}\:{dx}+\int{x}^{\mathrm{2}} \sqrt{{x}+\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\int{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{d}\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${I}_{\mathrm{2}} =\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:{use}\:{formula} \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\right) \\ $$$${I}_{\mathrm{3}} =\int\sqrt{{x}+\mathrm{1}}\:{dx} \\ $$$$=\frac{\left({x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${I}_{\mathrm{4}} =\int{x}^{\mathrm{2}} \sqrt{{x}+\mathrm{1}}\:{dx} \\ $$$${let}\:\:\:\:{t}^{\mathrm{2}} ={x}+\mathrm{1}\:\:\:\:\mathrm{2}{tdt}={dx} \\ $$$$\int\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ×{t}×\mathrm{2}{tdt} \\ $$$$\:\:\mathrm{2}\int{t}^{\mathrm{2}} \left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right){dt} \\ $$$$\mathrm{2}\int{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{4}} +{t}^{\mathrm{2}} \:\:{dt} \\ $$$$\mathrm{2}\left(\frac{{t}^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{2}{t}^{\mathrm{5}} }{\mathrm{5}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$$\frac{\mathrm{2}}{\mathrm{7}}\frac{{t}^{\mathrm{8}} }{\mathrm{8}}−\frac{\mathrm{4}}{\mathrm{5}}×\frac{{t}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{2}}{\mathrm{3}}×\frac{{t}^{\mathrm{4}} }{\mathrm{4}} \\ $$$$\frac{}{} \\ $$
Answered by MJS last updated on 25/Jul/18
∫x^2 (√(x+1))dx=(2/7)(x^2 −((4x)/5)+(8/(15)))(x+1)^(3/2) [((t=x+1 → dx=dt)),((∫(t−1)^2 (√t)dt=∫(t^2 −2t+1)(√t)dt=∫(t^(5/2) −2t^(3/2) +t^(1/2) )dt)),((∫t^q dt=(1/(q+1))t^(q+1) )) ] ∫x(√(x^2 +1))dx=(1/3)(x^2 +1)^(3/2) [((t=x^2 +1 → dx=(dt/(2x)))),(((1/2)∫(√t)dt)),((∫t^q dt=(1/(q+1))t^(q+1) )) ] ∫(√(x^2 +1))dx=(1/2)(x(√(x^2 +1))+ln∣x+(√(x^2 +1))∣) [((t=arctan x → dx=sec^2 t dt)),((∫sec^2 t (√(1+tan^2 t))dt=∫sec^3 t dt)),((∫sec^n t dt=((sec^(n−2) t tan t)/(n−1))+((n−2)/(n−1))∫sec^(n−2) t dt)) ] ∫(√(x+1))dx=(2/3)(x+1)^(3/2) [∫(x+a)^q dx=(1/(q+1))(x+a)^(q+1) ]
$$\int{x}^{\mathrm{2}} \sqrt{{x}+\mathrm{1}}{dx}=\frac{\mathrm{2}}{\mathrm{7}}\left({x}^{\mathrm{2}} −\frac{\mathrm{4}{x}}{\mathrm{5}}+\frac{\mathrm{8}}{\mathrm{15}}\right)\left({x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\begin{bmatrix}{{t}={x}+\mathrm{1}\:\rightarrow\:{dx}={dt}}\\{\int\left({t}−\mathrm{1}\right)^{\mathrm{2}} \sqrt{{t}}{dt}=\int\left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)\sqrt{{t}}{dt}=\int\left({t}^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{2}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} +{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \right){dt}}\\{\int{t}^{{q}} {dt}=\frac{\mathrm{1}}{{q}+\mathrm{1}}{t}^{{q}+\mathrm{1}} }\end{bmatrix} \\ $$$$\int{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\begin{bmatrix}{{t}={x}^{\mathrm{2}} +\mathrm{1}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}}}\\{\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{{t}}{dt}}\\{\int{t}^{{q}} {dt}=\frac{\mathrm{1}}{{q}+\mathrm{1}}{t}^{{q}+\mathrm{1}} }\end{bmatrix} \\ $$$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{ln}\mid{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\mid\right) \\ $$$$\:\:\:\:\:\begin{bmatrix}{{t}=\mathrm{arctan}\:{x}\:\rightarrow\:{dx}=\mathrm{sec}^{\mathrm{2}} \:{t}\:{dt}}\\{\int\mathrm{sec}^{\mathrm{2}} \:{t}\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt}=\int\mathrm{sec}^{\mathrm{3}} \:{t}\:{dt}}\\{\int\mathrm{sec}^{{n}} \:{t}\:{dt}=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \:{t}\:\mathrm{tan}\:{t}}{{n}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{t}\:{dt}}\end{bmatrix} \\ $$$$\int\sqrt{{x}+\mathrm{1}}{dx}=\frac{\mathrm{2}}{\mathrm{3}}\left({x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\left[\int\left({x}+{a}\right)^{{q}} {dx}=\frac{\mathrm{1}}{{q}+\mathrm{1}}\left({x}+{a}\right)^{{q}+\mathrm{1}} \right] \\ $$
Answered by maxmathsup by imad last updated on 25/Jul/18
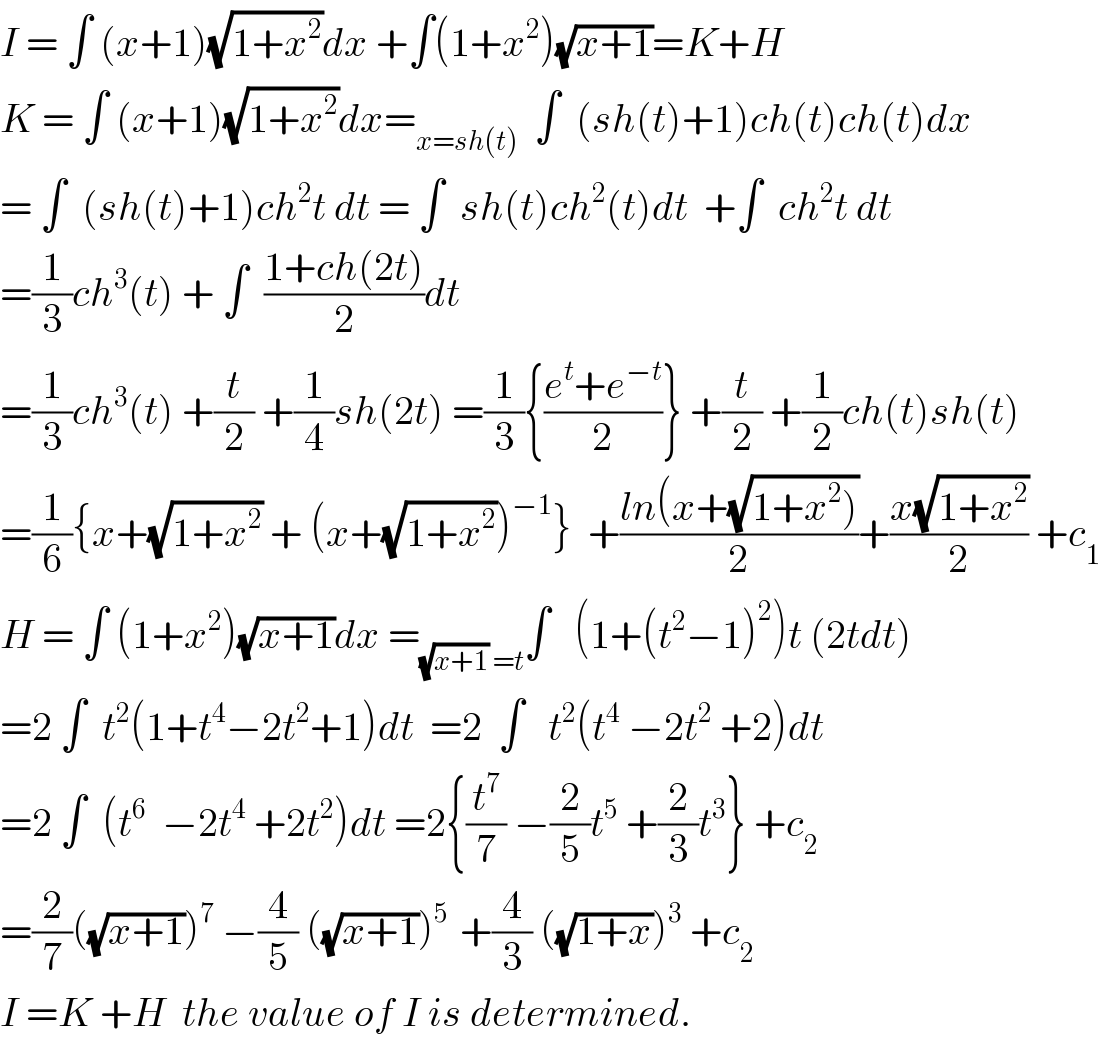
I = ∫ (x+1)(√(1+x^2 ))dx +∫(1+x^2 )(√(x+1))=K+H K = ∫ (x+1)(√(1+x^2 ))dx=_(x=sh(t)) ∫ (sh(t)+1)ch(t)ch(t)dx = ∫ (sh(t)+1)ch^2 t dt = ∫ sh(t)ch^2 (t)dt +∫ ch^2 t dt =(1/3)ch^3 (t) + ∫ ((1+ch(2t))/2)dt =(1/3)ch^3 (t) +(t/2) +(1/4)sh(2t) =(1/3){((e^t +e^(−t) )/2)} +(t/2) +(1/2)ch(t)sh(t) =(1/6){x+(√(1+x^2 )) + (x+(√(1+x^2 )))^(−1) } +((ln(x+(√(1+x^2 ))))/2)+((x(√(1+x^2 )))/2) +c_1 H = ∫ (1+x^2 )(√(x+1))dx =_((√(x+1)) =t) ∫ (1+(t^2 −1)^2 )t (2tdt) =2 ∫ t^2 (1+t^4 −2t^2 +1)dt =2 ∫ t^2 (t^4 −2t^2 +2)dt =2 ∫ (t^6 −2t^4 +2t^2 )dt =2{(t^7 /7) −(2/5)t^5 +(2/3)t^3 } +c_2 =(2/7)((√(x+1)))^7 −(4/5) ((√(x+1)))^(5 ) +(4/3) ((√(1+x)))^3 +c_2 I =K +H the value of I is determined.
$${I}\:=\:\int\:\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:+\int\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}+\mathrm{1}}={K}+{H} \\ $$$${K}\:=\:\int\:\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=_{{x}={sh}\left({t}\right)} \:\:\int\:\:\left({sh}\left({t}\right)+\mathrm{1}\right){ch}\left({t}\right){ch}\left({t}\right){dx} \\ $$$$=\:\int\:\:\left({sh}\left({t}\right)+\mathrm{1}\right){ch}^{\mathrm{2}} {t}\:{dt}\:=\:\int\:\:{sh}\left({t}\right){ch}^{\mathrm{2}} \left({t}\right){dt}\:\:+\int\:\:{ch}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ch}^{\mathrm{3}} \left({t}\right)\:+\:\int\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ch}^{\mathrm{3}} \left({t}\right)\:+\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}}\right\}\:+\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ch}\left({t}\right){sh}\left({t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{−\mathrm{1}} \right\}\:\:+\frac{{ln}\left({x}+\sqrt{\left.\mathrm{1}+{x}^{\mathrm{2}} \right)}\right.}{\mathrm{2}}+\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}}\:+{c}_{\mathrm{1}} \\ $$$${H}\:=\:\int\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}+\mathrm{1}}{dx}\:=_{\sqrt{{x}+\mathrm{1}}\:={t}} \int\:\:\:\left(\mathrm{1}+\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \right){t}\:\left(\mathrm{2}{tdt}\right) \\ $$$$=\mathrm{2}\:\int\:\:{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right){dt}\:\:=\mathrm{2}\:\:\int\:\:\:{t}^{\mathrm{2}} \left({t}^{\mathrm{4}} \:−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:\left({t}^{\mathrm{6}} \:\:−\mathrm{2}{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \right){dt}\:=\mathrm{2}\left\{\frac{{t}^{\mathrm{7}} }{\mathrm{7}}\:−\frac{\mathrm{2}}{\mathrm{5}}{t}^{\mathrm{5}} \:+\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \right\}\:+{c}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{7}}\left(\sqrt{{x}+\mathrm{1}}\right)^{\mathrm{7}} \:−\frac{\mathrm{4}}{\mathrm{5}}\:\left(\sqrt{{x}+\mathrm{1}}\right)^{\mathrm{5}\:} \:+\frac{\mathrm{4}}{\mathrm{3}}\:\left(\sqrt{\mathrm{1}+{x}}\right)^{\mathrm{3}} \:+{c}_{\mathrm{2}} \\ $$$${I}\:={K}\:+{H}\:\:{the}\:{value}\:{of}\:{I}\:{is}\:{determined}. \\ $$
Commented by maxmathsup by imad last updated on 25/Jul/18
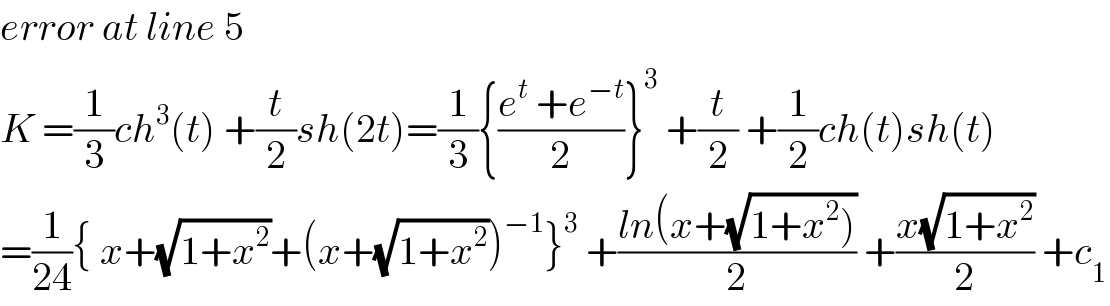
error at line 5 K =(1/3)ch^3 (t) +(t/2)sh(2t)=(1/3){((e^t +e^(−t) )/2)}^3 +(t/2) +(1/2)ch(t)sh(t) =(1/(24)){ x+(√(1+x^2 ))+(x+(√(1+x^2 )))^(−1) }^3 +((ln(x+(√(1+x^2 ))))/2) +((x(√(1+x^2 )))/2) +c_1
$${error}\:{at}\:{line}\:\mathrm{5} \\ $$$${K}\:=\frac{\mathrm{1}}{\mathrm{3}}{ch}^{\mathrm{3}} \left({t}\right)\:+\frac{{t}}{\mathrm{2}}{sh}\left(\mathrm{2}{t}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right\}^{\mathrm{3}} \:+\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ch}\left({t}\right){sh}\left({t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left\{\:{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{−\mathrm{1}} \right\}^{\mathrm{3}} \:+\frac{{ln}\left({x}+\sqrt{\left.\mathrm{1}+{x}^{\mathrm{2}} \right)}\right.}{\mathrm{2}}\:+\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}}\:+{c}_{\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *