Menu Close

find-x-1-cosx-dx-

Tinku Tara 0 Comments
Pin




Question Number 43914 by maxmathsup by imad last updated on 17/Sep/18
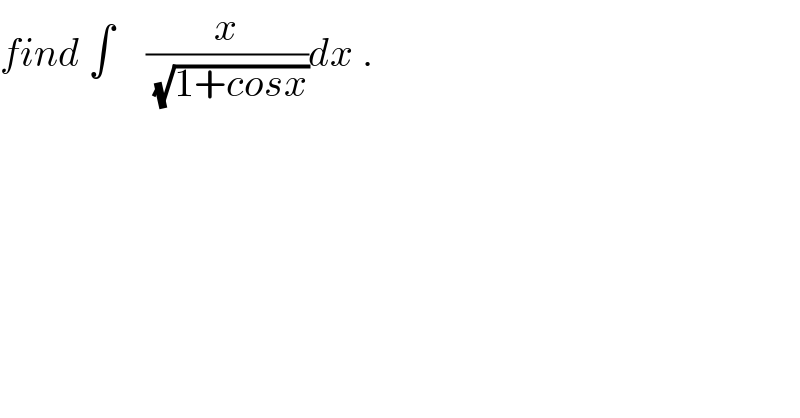
find ∫ (x/( (√(1+cosx))))dx .
$${find}\:\int\:\:\:\:\frac{{x}}{\:\sqrt{\mathrm{1}+{cosx}}}{dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 19/Sep/18
let A = ∫ (x/( (√(1+cosx))))dx we have A = ∫ (x/( (√(2cos^2 ((x/2))))))dx = (1/( (√2))) ∫ (x/(cos((x/2)))) dx =_((x/2)=t) (1/( (√2))) ∫ ((2t)/(cost)) 2dt=2(√2)∫ (t/(cost))dt =_(tan((t/2)) =u) 2(√2) ∫ ((2arctanu)/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) =8(√2) ∫ ((arctan(u))/(1−u^2 )) du let consider the parametric function f(α) = ∫ ((arctan(αu))/(1−u^2 ))du we have f^′ (α) = ∫ (u/((1−u^2 )(1+α^2 u^2 )))du let decompose F(u) =(u/((1−u^2 )(1+α^2 u^2 ))) =(a/(1−u)) +(b/(1+u)) +((cu +d)/(α^2 u^2 +1)) =(u/((1−u)(1+u)(α^2 u^2 +1))) a =lim_(u→1) (1−u)F(u) = (1/(2(1 +α^2 ))) b=lim_(u→−1) (1+u)F(u) = ((−1)/(2(1+α^2 ))) ⇒ F(u) = (1/(2(1+α^2 )(1−u))) −(1/(2(1+α^2 )(1+u))) +((cu +d)/(α^2 u^2 +1)) lim_(u→+∞) uF(u) =0 =−a +b +(c/α^2 ) ⇒(c/α^2 ) =a−b =(1/(2(1+α^2 ))) +(1/(2(1+α^2 ))) = (1/(1+α^2 )) ⇒c =(α^2 /(1+α^2 )) ⇒F(u)= (1/(2(1+α^2 )(1−u))) −(1/(2(1+α^2 )(1+u))) +(((α^2 /(1+α^2 ))u +d)/(1+α^2 u^2 )) F(o)=0 =d ⇒ ∫ F(u)du =(1/(2(1+α^2 ))) ∫ ((1/(1−u))−(1/(1+u)))du + (α^2 /(1+α^2 )) ∫ (u/(1+α^2 u^2 )) du but ∫((1/(1−u)) −(1/(1+u)))du =−ln∣1−u^2 ∣ +c_1 (1/(1+α^2 ))∫ ((α^2 u)/(1+α^2 u^2 ))du =(1/(2(1+α^2 )))ln∣1+α^2 u^2 ∣ +c_2 ⇒ f^′ (α) =−((ln∣1−u^2 ∣)/(2(1+α^2 ))) + (1/(2(1+α^2 )))ln∣1+α^2 u^2 ∣ +k .....be continued...
$${let}\:{A}\:=\:\int\:\:\:\:\:\frac{{x}}{\:\sqrt{\mathrm{1}+{cosx}}}{dx}\:{we}\:{have}\:{A}\:=\:\int\:\:\:\frac{{x}}{\:\sqrt{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\:\frac{{x}}{{cos}\left(\frac{{x}}{\mathrm{2}}\right)}\:{dx}\:=_{\frac{{x}}{\mathrm{2}}={t}} \:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{\mathrm{2}{t}}{{cost}}\:\:\mathrm{2}{dt}=\mathrm{2}\sqrt{\mathrm{2}}\int\:\:\:\frac{{t}}{{cost}}{dt} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={u}} \:\:\:\mathrm{2}\sqrt{\mathrm{2}}\:\int\:\:\:\:\:\frac{\mathrm{2}{arctanu}}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{8}\sqrt{\mathrm{2}}\:\int\:\:\:\:\:\frac{{arctan}\left({u}\right)}{\mathrm{1}−{u}^{\mathrm{2}} }\:{du} \\ $$$${let}\:{consider}\:{the}\:{parametric}\:{function}\:{f}\left(\alpha\right)\:=\:\int\:\:\:\:\frac{{arctan}\left(\alpha{u}\right)}{\mathrm{1}−{u}^{\mathrm{2}} }{du} \\ $$$${we}\:{have}\:{f}^{'} \left(\alpha\right)\:=\:\int\:\:\:\:\:\frac{{u}}{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \right)}{du}\:{let}\:{decompose}\: \\ $$$${F}\left({u}\right)\:=\frac{{u}}{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \right)}\:=\frac{{a}}{\mathrm{1}−{u}}\:+\frac{{b}}{\mathrm{1}+{u}}\:+\frac{{cu}\:+{d}}{\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{{u}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}\right)\left(\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${a}\:={lim}_{{u}\rightarrow\mathrm{1}} \left(\mathrm{1}−{u}\right){F}\left({u}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}\:+\alpha^{\mathrm{2}} \right)} \\ $$$${b}={lim}_{{u}\rightarrow−\mathrm{1}} \left(\mathrm{1}+{u}\right){F}\left({u}\right)\:=\:\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\mathrm{1}−{u}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right)}\:+\frac{{cu}\:+{d}}{\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)\:=\mathrm{0}\:=−{a}\:+{b}\:+\frac{{c}}{\alpha^{\mathrm{2}} }\:\Rightarrow\frac{{c}}{\alpha^{\mathrm{2}} }\:={a}−{b}\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\:\Rightarrow{c}\:=\frac{\alpha^{\mathrm{2}} }{\mathrm{1}+\alpha^{\mathrm{2}} }\:\Rightarrow{F}\left({u}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\mathrm{1}−{u}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right)}\:+\frac{\frac{\alpha^{\mathrm{2}} }{\mathrm{1}+\alpha^{\mathrm{2}} }{u}\:+{d}}{\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$${F}\left({o}\right)=\mathrm{0}\:={d}\:\Rightarrow\:\int\:\:{F}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$$+\:\frac{\alpha^{\mathrm{2}} }{\mathrm{1}+\alpha^{\mathrm{2}} }\:\int\:\:\:\:\:\:\frac{{u}}{\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} }\:{du}\:{but}\:\int\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}\:−\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du}\:=−{ln}\mid\mathrm{1}−{u}^{\mathrm{2}} \mid\:+{c}_{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\int\:\:\:\:\frac{\alpha^{\mathrm{2}} {u}}{\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} }{du}\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\mid\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \mid\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$${f}^{'} \left(\alpha\right)\:=−\frac{{ln}\mid\mathrm{1}−{u}^{\mathrm{2}} \mid}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\mid\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \mid\:+{k}\:\:…..{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *