Question Number 192676 by Shrinava last updated on 24/May/23
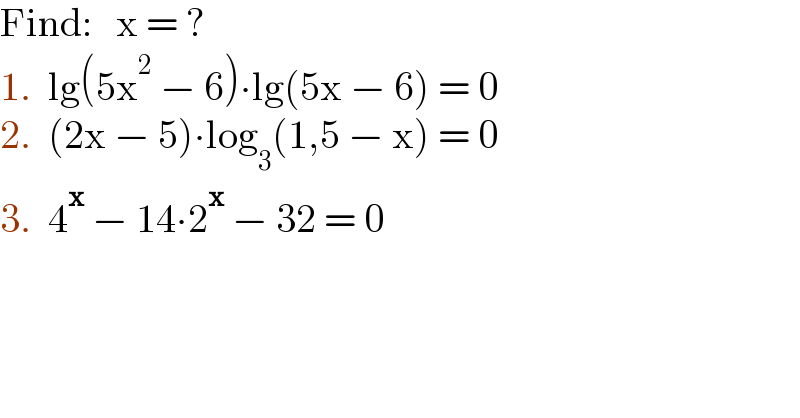
$$\mathrm{Find}:\:\:\:\mathrm{x}\:=\:? \\ $$$$\mathrm{1}.\:\:\mathrm{lg}\left(\mathrm{5x}^{\mathrm{2}} \:−\:\mathrm{6}\right)\centerdot\mathrm{lg}\left(\mathrm{5x}\:−\:\mathrm{6}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{2}.\:\:\left(\mathrm{2x}\:−\:\mathrm{5}\right)\centerdot\mathrm{log}_{\mathrm{3}} \left(\mathrm{1},\mathrm{5}\:−\:\mathrm{x}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{3}.\:\:\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{14}\centerdot\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:−\:\mathrm{32}\:=\:\mathrm{0} \\ $$
Answered by Frix last updated on 24/May/23
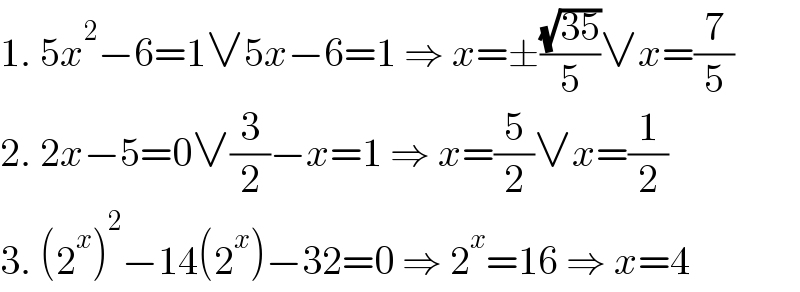
$$\mathrm{1}.\:\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}=\mathrm{1}\vee\mathrm{5}{x}−\mathrm{6}=\mathrm{1}\:\Rightarrow\:{x}=\pm\frac{\sqrt{\mathrm{35}}}{\mathrm{5}}\vee{x}=\frac{\mathrm{7}}{\mathrm{5}} \\ $$$$\mathrm{2}.\:\mathrm{2}{x}−\mathrm{5}=\mathrm{0}\vee\frac{\mathrm{3}}{\mathrm{2}}−{x}=\mathrm{1}\:\Rightarrow\:{x}=\frac{\mathrm{5}}{\mathrm{2}}\vee{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}.\:\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} −\mathrm{14}\left(\mathrm{2}^{{x}} \right)−\mathrm{32}=\mathrm{0}\:\Rightarrow\:\mathrm{2}^{{x}} =\mathrm{16}\:\Rightarrow\:{x}=\mathrm{4} \\ $$
