Menu Close

find-x-2-1-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 63822 by mathmax by abdo last updated on 09/Jul/19
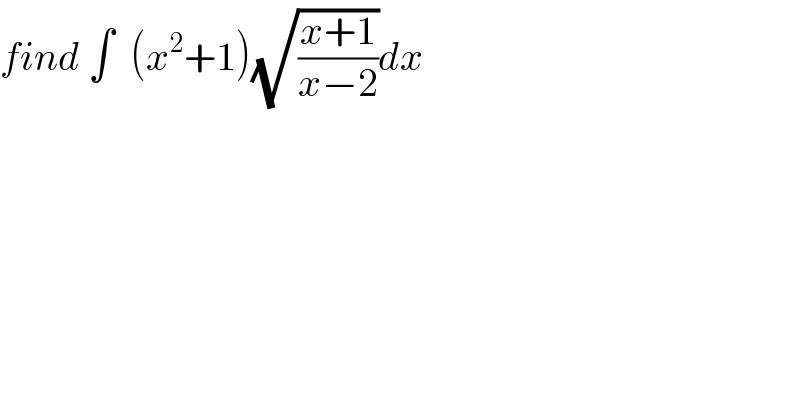
find ∫ (x^2 +1)(√((x+1)/(x−2)))dx
find∫(x2+1)x+1x−2dx
Commented by mathmax by abdo last updated on 11/Jul/19
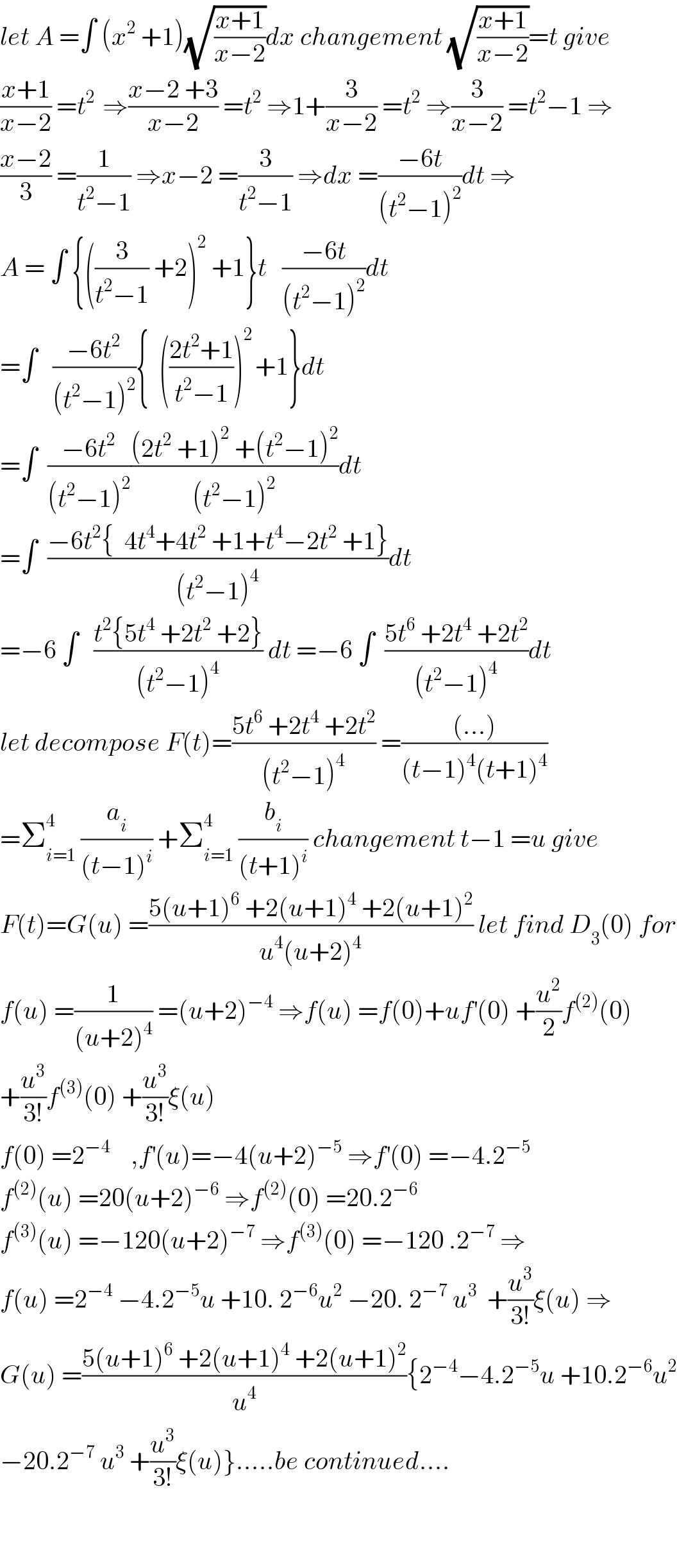
let A =∫ (x^2 +1)(√((x+1)/(x−2)))dx changement (√((x+1)/(x−2)))=t give ((x+1)/(x−2)) =t^(2 ) ⇒((x−2 +3)/(x−2)) =t^2 ⇒1+(3/(x−2)) =t^2 ⇒(3/(x−2)) =t^2 −1 ⇒ ((x−2)/3) =(1/(t^2 −1)) ⇒x−2 =(3/(t^2 −1)) ⇒dx =((−6t)/((t^2 −1)^2 ))dt ⇒ A = ∫ {((3/(t^2 −1)) +2)^2 +1}t ((−6t)/((t^2 −1)^2 ))dt =∫ ((−6t^2 )/((t^2 −1)^2 )){ (((2t^2 +1)/(t^2 −1)))^(2 ) +1}dt =∫ ((−6t^2 )/((t^2 −1)^2 ))(((2t^2 +1)^2 +(t^2 −1)^2 )/((t^2 −1)^2 ))dt =∫ ((−6t^2 { 4t^4 +4t^2 +1+t^4 −2t^2 +1})/((t^2 −1)^4 ))dt =−6 ∫ ((t^2 {5t^4 +2t^2 +2})/((t^2 −1)^4 )) dt =−6 ∫ ((5t^6 +2t^4 +2t^2 )/((t^2 −1)^4 ))dt let decompose F(t)=((5t^6 +2t^4 +2t^2 )/((t^2 −1)^4 )) =(((...))/((t−1)^4 (t+1)^4 )) =Σ_(i=1) ^4 (a_i /((t−1)^i )) +Σ_(i=1) ^4 (b_i /((t+1)^i )) changement t−1 =u give F(t)=G(u) =((5(u+1)^6 +2(u+1)^4 +2(u+1)^2 )/(u^4 (u+2)^4 )) let find D_3 (0) for f(u) =(1/((u+2)^4 )) =(u+2)^(−4) ⇒f(u) =f(0)+uf^′ (0) +(u^2 /2)f^((2)) (0) +(u^3 /(3!))f^((3)) (0) +(u^3 /(3!))ξ(u) f(0) =2^(−4) ,f^′ (u)=−4(u+2)^(−5) ⇒f^′ (0) =−4.2^(−5) f^((2)) (u) =20(u+2)^(−6) ⇒f^((2)) (0) =20.2^(−6) f^((3)) (u) =−120(u+2)^(−7) ⇒f^((3)) (0) =−120 .2^(−7) ⇒ f(u) =2^(−4) −4.2^(−5) u +10. 2^(−6) u^2 −20. 2^(−7) u^3 +(u^3 /(3!))ξ(u) ⇒ G(u) =((5(u+1)^6 +2(u+1)^4 +2(u+1)^2 )/u^4 ){2^(−4) −4.2^(−5) u +10.2^(−6) u^2 −20.2^(−7) u^3 +(u^3 /(3!))ξ(u)}.....be continued....
letA=∫(x2+1)x+1x−2dxchangementx+1x−2=tgivex+1x−2=t2⇒x−2+3x−2=t2⇒1+3x−2=t2⇒3x−2=t2−1⇒x−23=1t2−1⇒x−2=3t2−1⇒dx=−6t(t2−1)2dt⇒A=∫{(3t2−1+2)2+1}t−6t(t2−1)2dt=∫−6t2(t2−1)2{(2t2+1t2−1)2+1}dt=∫−6t2(t2−1)2(2t2+1)2+(t2−1)2(t2−1)2dt=∫−6t2{4t4+4t2+1+t4−2t2+1}(t2−1)4dt=−6∫t2{5t4+2t2+2}(t2−1)4dt=−6∫5t6+2t4+2t2(t2−1)4dtletdecomposeF(t)=5t6+2t4+2t2(t2−1)4=(…)(t−1)4(t+1)4=∑i=14ai(t−1)i+∑i=14bi(t+1)ichangementt−1=ugiveF(t)=G(u)=5(u+1)6+2(u+1)4+2(u+1)2u4(u+2)4letfindD3(0)forf(u)=1(u+2)4=(u+2)−4⇒f(u)=f(0)+uf′(0)+u22f(2)(0)+u33!f(3)(0)+u33!ξ(u)f(0)=2−4,f′(u)=−4(u+2)−5⇒f′(0)=−4.2−5f(2)(u)=20(u+2)−6⇒f(2)(0)=20.2−6f(3)(u)=−120(u+2)−7⇒f(3)(0)=−120.2−7⇒f(u)=2−4−4.2−5u+10.2−6u2−20.2−7u3+u33!ξ(u)⇒G(u)=5(u+1)6+2(u+1)4+2(u+1)2u4{2−4−4.2−5u+10.2−6u2−20.2−7u3+u33!ξ(u)}…..becontinued….

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *