find-x-2-2-findx-

Question Number 96241 by joki last updated on 30/May/20

find x^{2} = 2^{\times} findx ?

Answered by 1549442205 last updated on 31/May/20

It is easy to see that x \in {0, 1} {don}^{'} t satisfy

and x \in {2, 4} satisfying the given equation

We prove that 2^{x} > x^{2} for any x ⩾ 5

Indeed, consider the function f (x) =

2^{x} - x^{2} . We have f^{'} (x) = 2^{x} \ln 2 - 2 x,

f^{″} (x) = 2^{x} \ln^{2} 2 - 2 > {32 \ln}^{2} 2 - 2 > 0

Hence, f^{'} (x) is increasing function on

] 5; + \infty) \Rightarrow f^{'} (x) > f^{'} (5) = 32 \ln 2 - 10 > 0

This show that

the function f (x) = 2^{x} - x^{2} is increasing

on [5; + \infty) \Rightarrow f (x) > f (5) = 2^{5} - 25 > 0

\Rightarrow 2^{x} - x^{2} > 0 \Rightarrow 2^{x} > x^{2} for every x ⩾ 5 .

Thus, the numbers x satisfy the given

equation are x \in {2; 4}

Answered by mr W last updated on 31/May/20

x^{2} = 2^{x}

\Rightarrow x = \pm 2^{\frac{x}{2}} = \pm e^{\frac{x}{2} \ln 2}

\Rightarrow {x e}^{- \frac{x}{2} \ln 2} = \pm 1

\Rightarrow (- \frac{x}{2} \ln 2) e^{- \frac{x}{2} \ln 2} = \pm \frac{\ln 2}{2}

\Rightarrow - \frac{x}{2} \ln 2 = W (\pm \frac{\ln 2}{2}) w i t h W () = L a m b e r t W f u n c t i o n

\Rightarrow x = - (\frac{2}{\ln 2}) W (\pm \frac{\ln 2}{2}) = {\begin{cases} - \frac{2}{\ln 2} W (\frac{\ln 2}{2}) \approx - \frac{2}{\ln 2} \times 0.26570574 = - 0.766665 \\ - \frac{2}{\ln 2} W (- \frac{\ln 2}{2}) = {\begin{cases} - \frac{2}{\ln 2} \times (- 0.693147) = 2 \\ - \frac{2}{\ln 2} \times (- 1.386294) = 4 \end{cases} \end{cases}

t h a t m e a n s t h e r e a r e t h r e e r o o t s .

Commented by mr W last updated on 31/May/20

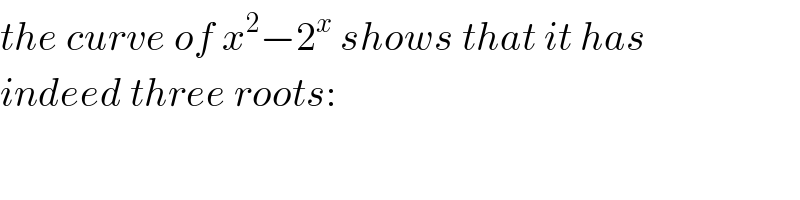
t h e c u r v e o f x^{2} - 2^{x} s h o w s t h a t i t h a s

i n d e e d t h r e e r o o t s :

Commented by mr W last updated on 31/May/20

Facebook Tweet Pin