Question Number 29441 by prof Abdo imad last updated on 08/Feb/18
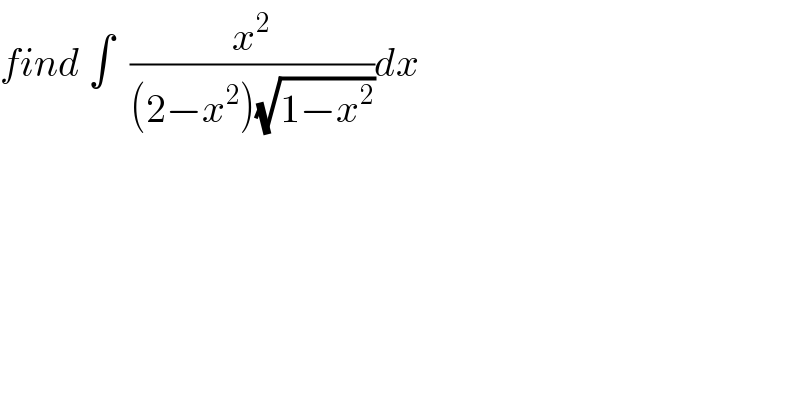
$${find}\:\int\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$
Commented by prof Abdo imad last updated on 07/Mar/18

$${I}\:=−\int\:\frac{\mathrm{2}−{x}^{\mathrm{2}} \:−\mathrm{2}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\:−\int\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+\mathrm{2}\int\:\:\:\frac{{dx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=−{arcsinx}\:+\mathrm{2}\:\int\:\:\:\:\frac{{dx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{the}\:{ch}.{x}={sint}\Rightarrow \\ $$$$\int\:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\int\:\:\:\:\frac{{cost}\:{dt}}{\left(\mathrm{2}−{sin}^{\mathrm{2}} {t}\right){cost}} \\ $$$$=\:\int\:\:\:\:\frac{{dt}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}\:=\int\:\:\:\:\frac{{dt}}{\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}} \\ $$$$=\:\int\:\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}\:{and}\:{tbe}\:{type}\:{of}\:{this}\:{integral} \\ $$$${is}\:{calculated}…. \\ $$
