Question Number 57750 by maxmathsup by imad last updated on 11/Apr/19
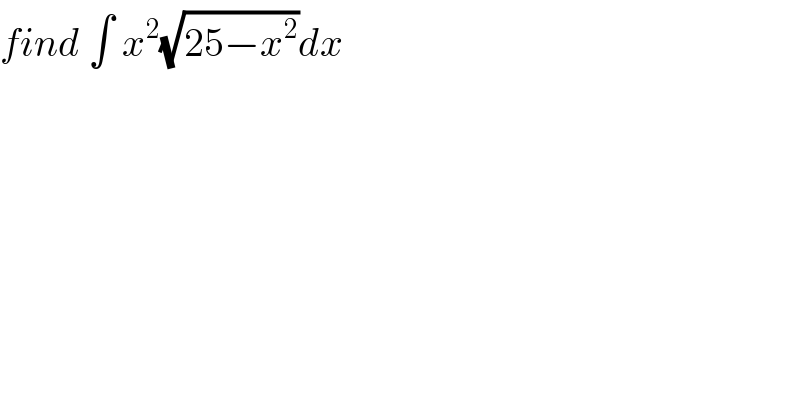
$${find}\:\int\:{x}^{\mathrm{2}} \sqrt{\mathrm{25}−{x}^{\mathrm{2}} }{dx}\: \\ $$
Answered by MJS last updated on 11/Apr/19
![∫x^2 (√(25−x^2 ))dx= [t=sin^(−1) (x/5) → dx=5cos t dt] =625∫sin^2 t cos^2 t dt=((625)/8)∫(1−cos 4t)dt= =((625)/8)t−((625)/(32))sin 4t =((625)/8)sin^(−1) (x/5) −((625)/(32))sin (4sin^(−1) (x/5)) = =((625)/8)sin^(−1) (x/5) +(1/8)x(2x^2 −25)(√(25−x^2 )) +C](https://www.tinkutara.com/question/Q57763.png)
$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{25}−{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{5}}\:\rightarrow\:{dx}=\mathrm{5cos}\:{t}\:{dt}\right] \\ $$$$=\mathrm{625}\int\mathrm{sin}^{\mathrm{2}} \:{t}\:\mathrm{cos}^{\mathrm{2}} \:{t}\:{dt}=\frac{\mathrm{625}}{\mathrm{8}}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{4}{t}\right){dt}= \\ $$$$=\frac{\mathrm{625}}{\mathrm{8}}{t}−\frac{\mathrm{625}}{\mathrm{32}}\mathrm{sin}\:\mathrm{4}{t}\:=\frac{\mathrm{625}}{\mathrm{8}}\mathrm{sin}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{5}}\:−\frac{\mathrm{625}}{\mathrm{32}}\mathrm{sin}\:\left(\mathrm{4sin}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{5}}\right)\:= \\ $$$$=\frac{\mathrm{625}}{\mathrm{8}}\mathrm{sin}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{5}}\:+\frac{\mathrm{1}}{\mathrm{8}}{x}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{25}\right)\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\:+{C} \\ $$
Commented by maxmathsup by imad last updated on 11/Apr/19

$${thanks}\:{sir}\:{mjs} \\ $$
