Menu Close

find-x-2-4-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 57748 by maxmathsup by imad last updated on 11/Apr/19
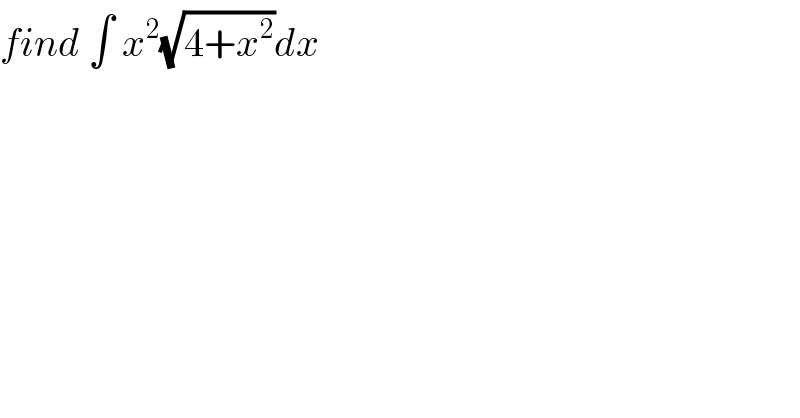
find ∫ x^2 (√(4+x^2 ))dx
$${find}\:\int\:{x}^{\mathrm{2}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }{dx} \\ $$
Commented by maxmathsup by imad last updated on 11/Apr/19
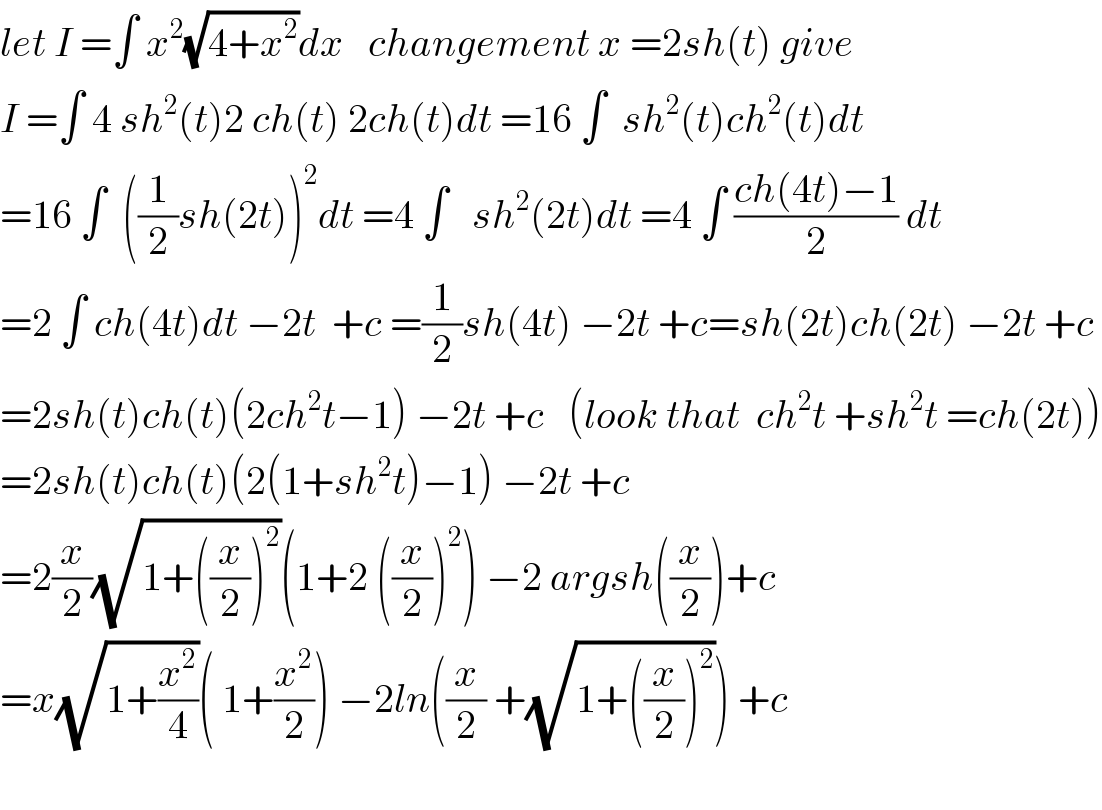
let I =∫ x^2 (√(4+x^2 ))dx changement x =2sh(t) give I =∫ 4 sh^2 (t)2 ch(t) 2ch(t)dt =16 ∫ sh^2 (t)ch^2 (t)dt =16 ∫ ((1/2)sh(2t))^2 dt =4 ∫ sh^2 (2t)dt =4 ∫ ((ch(4t)−1)/2) dt =2 ∫ ch(4t)dt −2t +c =(1/2)sh(4t) −2t +c=sh(2t)ch(2t) −2t +c =2sh(t)ch(t)(2ch^2 t−1) −2t +c (look that ch^2 t +sh^2 t =ch(2t)) =2sh(t)ch(t)(2(1+sh^2 t)−1) −2t +c =2(x/2)(√(1+((x/2))^2 ))(1+2 ((x/2))^2 ) −2 argsh((x/2))+c =x(√(1+(x^2 /4)))( 1+(x^2 /2)) −2ln((x/2) +(√(1+((x/2))^2 ))) +c
$${let}\:{I}\:=\int\:{x}^{\mathrm{2}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:\:\:{changement}\:{x}\:=\mathrm{2}{sh}\left({t}\right)\:{give} \\ $$$${I}\:=\int\:\mathrm{4}\:{sh}^{\mathrm{2}} \left({t}\right)\mathrm{2}\:{ch}\left({t}\right)\:\mathrm{2}{ch}\left({t}\right){dt}\:=\mathrm{16}\:\int\:\:{sh}^{\mathrm{2}} \left({t}\right){ch}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$=\mathrm{16}\:\int\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} {dt}\:=\mathrm{4}\:\int\:\:\:{sh}^{\mathrm{2}} \left(\mathrm{2}{t}\right){dt}\:=\mathrm{4}\:\int\:\frac{{ch}\left(\mathrm{4}{t}\right)−\mathrm{1}}{\mathrm{2}}\:{dt} \\ $$$$=\mathrm{2}\:\int\:{ch}\left(\mathrm{4}{t}\right){dt}\:−\mathrm{2}{t}\:\:+{c}\:=\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{4}{t}\right)\:−\mathrm{2}{t}\:+{c}={sh}\left(\mathrm{2}{t}\right){ch}\left(\mathrm{2}{t}\right)\:−\mathrm{2}{t}\:+{c} \\ $$$$=\mathrm{2}{sh}\left({t}\right){ch}\left({t}\right)\left(\mathrm{2}{ch}^{\mathrm{2}} {t}−\mathrm{1}\right)\:−\mathrm{2}{t}\:+{c}\:\:\:\left({look}\:{that}\:\:{ch}^{\mathrm{2}} {t}\:+{sh}^{\mathrm{2}} {t}\:={ch}\left(\mathrm{2}{t}\right)\right) \\ $$$$=\mathrm{2}{sh}\left({t}\right){ch}\left({t}\right)\left(\mathrm{2}\left(\mathrm{1}+{sh}^{\mathrm{2}} {t}\right)−\mathrm{1}\right)\:−\mathrm{2}{t}\:+{c}\: \\ $$$$=\mathrm{2}\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}+\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{2}\:\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \right)\:−\mathrm{2}\:{argsh}\left(\frac{{x}}{\mathrm{2}}\right)+{c} \\ $$$$={x}\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\left(\:\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:−\mathrm{2}{ln}\left(\frac{{x}}{\mathrm{2}}\:+\sqrt{\mathrm{1}+\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\right)\:+{c} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 11/Apr/19
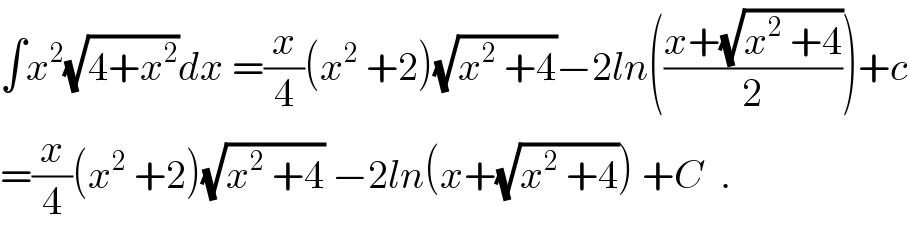
∫x^2 (√(4+x^2 ))dx =(x/4)(x^2 +2)(√(x^2 +4))−2ln(((x+(√(x^2 +4)))/2))+c =(x/4)(x^2 +2)(√(x^2 +4)) −2ln(x+(√(x^2 +4))) +C .
$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:=\frac{{x}}{\mathrm{4}}\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}−\mathrm{2}{ln}\left(\frac{{x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}}{\mathrm{2}}\right)+{c} \\ $$$$=\frac{{x}}{\mathrm{4}}\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}\:−\mathrm{2}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}}\right)\:+{C}\:\:. \\ $$
Answered by MJS last updated on 11/Apr/19
∫x^2 (√(x^2 +4))dx= [t=sinh^(−1) (x/2) → dx=2cosh t dt] =16∫sinh^2 t cosh^2 t dt=−2∫(1−cosh 4t)dt= =−2∫dt+2∫cosh 4t dt=−2t+(1/2)sinh 4t= =−2sinh^(−1) (x/2) +(1/2)sinh (4sinh^(−1) (x/2)) +C
$$\int{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{4}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\mathrm{2cosh}\:{t}\:{dt}\right] \\ $$$$=\mathrm{16}\int\mathrm{sinh}^{\mathrm{2}} \:{t}\:\mathrm{cosh}^{\mathrm{2}} \:{t}\:{dt}=−\mathrm{2}\int\left(\mathrm{1}−\mathrm{cosh}\:\mathrm{4}{t}\right){dt}= \\ $$$$=−\mathrm{2}\int{dt}+\mathrm{2}\int\mathrm{cosh}\:\mathrm{4}{t}\:{dt}=−\mathrm{2}{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh}\:\mathrm{4}{t}= \\ $$$$=−\mathrm{2sinh}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinh}\:\left(\mathrm{4sinh}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$
Commented by MJS last updated on 11/Apr/19
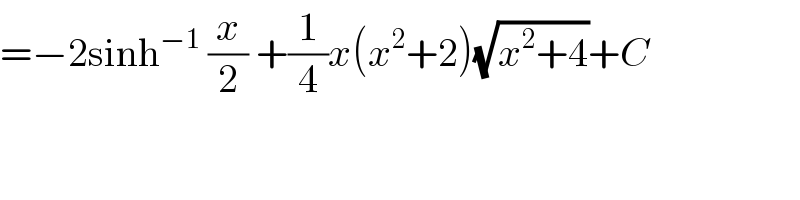
=−2sinh^(−1) (x/2) +(1/4)x(x^2 +2)(√(x^2 +4))+C
$$=−\mathrm{2sinh}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}+{C} \\ $$
Answered by MJS last updated on 11/Apr/19
∫x^2 (√(x^2 +4))dx= [t=tan^(−1) (x/2) → dx=2sec^2 t dt] =16∫(sec^5 t −sec^3 t)dt= [∫sec^n t dt=((sec^(n−2) t tan t)/(t−1))+((n−2)/(n−1))∫sec^(n−2) t dt] =−2ln (tan t +sec t) +sec t (1−2tan t (1−2sec^2 t))= =(1/4)x(x^2 +2)(√(x^2 +4))−2ln ∣x+(√(x^2 +4))∣ +C
$$\int{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{4}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}^{−\mathrm{1}} \:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\mathrm{2sec}^{\mathrm{2}} \:{t}\:{dt}\right] \\ $$$$=\mathrm{16}\int\left(\mathrm{sec}^{\mathrm{5}} \:{t}\:−\mathrm{sec}^{\mathrm{3}} \:{t}\right){dt}= \\ $$$$\:\:\:\:\:\left[\int\mathrm{sec}^{{n}} \:{t}\:{dt}=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \:{t}\:\mathrm{tan}\:{t}}{{t}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{t}\:{dt}\right] \\ $$$$=−\mathrm{2ln}\:\left(\mathrm{tan}\:{t}\:+\mathrm{sec}\:{t}\right)\:+\mathrm{sec}\:{t}\:\left(\mathrm{1}−\mathrm{2tan}\:{t}\:\left(\mathrm{1}−\mathrm{2sec}^{\mathrm{2}} \:{t}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2ln}\:\mid{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\mid\:+{C} \\ $$
Commented by maxmathsup by imad last updated on 11/Apr/19
thanks sir mjs
$${thanks}\:{sir}\:{mjs} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *