Menu Close

find-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 47018 by maxmathsup by imad last updated on 03/Nov/18
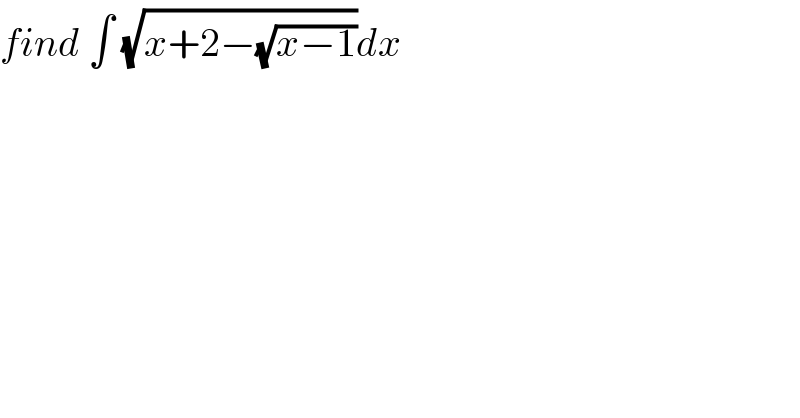
find ∫ (√(x+2−(√(x−1))))dx
$${find}\:\int\:\sqrt{{x}+\mathrm{2}−\sqrt{{x}−\mathrm{1}}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 04/Nov/18
let A = ∫(√(x+2−(√(x−1))))dx changement (√(x−1))=t give A =∫ (√(1+t^2 +2−t))(2t)dt =2 ∫ t(√(t^2 −t+3))dt but t^2 −t +3 =(t−(1/2))^2 +3−(1/4) =(t−(1/2))^2 +((11)/4) ⇒A=_(t−(1/2)=((√(11))/2)u) ∫((1/2)+((√(11))/2)u)((√(11))/2)(√(1+u^2 ))((√(11))/2)du =((11)/4) ∫ (1+(√(11))u)(√(1+u^2 ))du ⇒(4/(11)) A =_(u =shα) ∫ (1+(√(11))shα)chαchα dα =∫ ch^2 α dα +(√(11))∫ shα ch^2 α dα =∫ ((1+ch(2α))/2)dα +((√(11))/3) ch^3 α +C =(α/2) +(1/4)sh(α) +((√(11))/3)ch^3 α +C =((argsh(u))/2) +(u/4) + ((√(11))/3) ch^3 (argsh(u)) +C =(1/2)ln(u+(√(1+u^2 ))) +(u/4) +((√(11))/3) ch^3 (ln(u+(√(1+u^2 ))) +C =(1/2)ln(((2t−1)/( (√(11)))) +(√(1+(((2t−1)/( (√(11)))))^2 ))) +((2t−1)/(4(√(11)))) +((√(11))/3)ch^3 (ln(((2t−1)/( (√(11)))) +(√(1+(((2t−1)/( (√(11)))))))) +C with t =(√(x−1)).
$${let}\:{A}\:=\:\int\sqrt{{x}+\mathrm{2}−\sqrt{{x}−\mathrm{1}}}{dx}\:\:{changement}\:\sqrt{{x}−\mathrm{1}}={t}\:{give} \\ $$$${A}\:=\int\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}−{t}}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int\:\:{t}\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{3}}{dt}\:{but}\: \\ $$$${t}^{\mathrm{2}} −{t}\:+\mathrm{3}\:=\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{11}}{\mathrm{4}}\:\Rightarrow{A}=_{{t}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{u}} \:\int\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{u}\right)\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{11}}{\mathrm{4}}\:\int\:\left(\mathrm{1}+\sqrt{\mathrm{11}}{u}\right)\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:\Rightarrow\frac{\mathrm{4}}{\mathrm{11}}\:{A}\:=_{{u}\:={sh}\alpha} \:\int\:\:\left(\mathrm{1}+\sqrt{\mathrm{11}}{sh}\alpha\right){ch}\alpha{ch}\alpha\:{d}\alpha \\ $$$$=\int\:{ch}^{\mathrm{2}} \alpha\:{d}\alpha\:+\sqrt{\mathrm{11}}\int\:{sh}\alpha\:{ch}^{\mathrm{2}} \alpha\:{d}\alpha \\ $$$$=\int\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}{d}\alpha\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\:{ch}^{\mathrm{3}} \alpha\:+{C}\:=\frac{\alpha}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\alpha\right)\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}{ch}^{\mathrm{3}} \alpha\:+{C} \\ $$$$=\frac{{argsh}\left({u}\right)}{\mathrm{2}}\:+\frac{{u}}{\mathrm{4}}\:+\:\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\:{ch}^{\mathrm{3}} \left({argsh}\left({u}\right)\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:+\frac{{u}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}\:{ch}^{\mathrm{3}} \left({ln}\left({u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:+{C}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{2}{t}−\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{11}}}\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{3}}{ch}^{\mathrm{3}} \left({ln}\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{11}}}\right)}\right)\:+{C}\right. \\ $$$${with}\:{t}\:=\sqrt{{x}−\mathrm{1}}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Nov/18
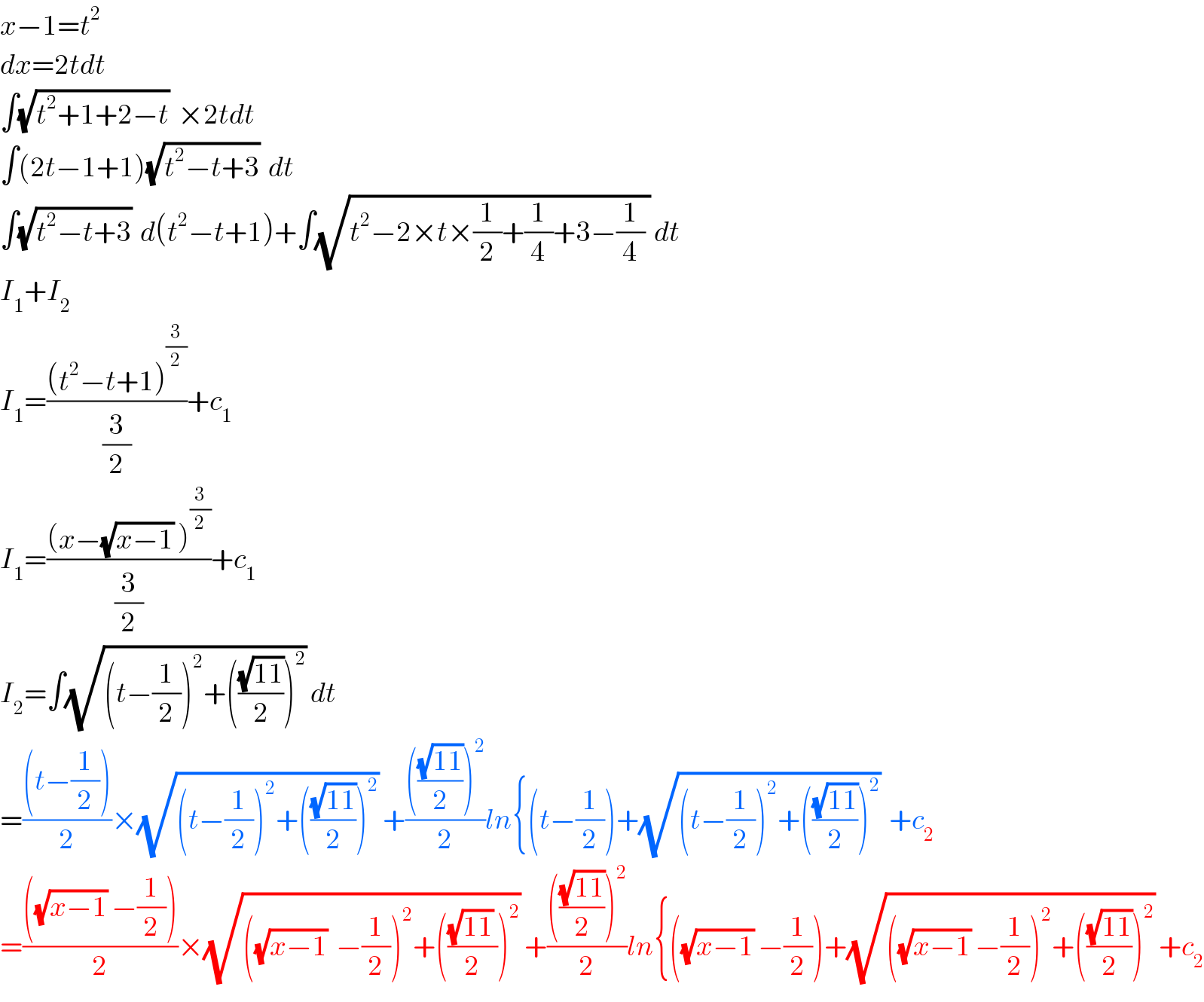
x−1=t^2 dx=2tdt ∫(√(t^2 +1+2−t)) ×2tdt ∫(2t−1+1)(√(t^2 −t+3)) dt ∫(√(t^2 −t+3)) d(t^2 −t+1)+∫(√(t^2 −2×t×(1/2)+(1/4)+3−(1/4) )) dt I_1 +I_2 I_1 =(((t^2 −t+1)^(3/2) )/(3/2))+c_1 I_1 =(((x−(√(x−1)) )^(3/2) )/(3/2))+c_1 I_2 =∫(√((t−(1/2))^2 +(((√(11))/2))^2 )) dt =(((t−(1/2)))/2)×(√((t−(1/2))^2 +(((√(11))/2))^2 )) +(((((√(11))/2))^2 )/2)ln{(t−(1/2))+(√((t−(1/2))^2 +(((√(11))/2))^2 )) +c_2 =((((√(x−1)) −(1/2)))/2)×(√(((√(x−1)) −(1/2))^2 +((((√(11)) )/2))^2 )) +(((((√(11))/2))^2 )/2)ln{((√(x−1)) −(1/2))+(√(((√(x−1)) −(1/2))^2 +(((√(11))/2))^2 )) +c_2
$${x}−\mathrm{1}={t}^{\mathrm{2}} \\ $$$${dx}=\mathrm{2}{tdt} \\ $$$$\int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}−{t}}\:\:×\mathrm{2}{tdt} \\ $$$$\int\left(\mathrm{2}{t}−\mathrm{1}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{3}}\:\:{dt} \\ $$$$\int\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{3}}\:\:{d}\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)+\int\sqrt{{t}^{\mathrm{2}} −\mathrm{2}×{t}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}\:}\:{dt} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\frac{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\mathrm{3}}{\mathrm{2}}}+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\frac{\left({x}−\sqrt{{x}−\mathrm{1}}\:\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\mathrm{3}}{\mathrm{2}}}+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\int\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dt} \\ $$$$=\frac{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}×\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\frac{\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left\{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\:+{c}_{\mathrm{2}} \right. \\ $$$$=\frac{\left(\sqrt{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}×\sqrt{\left(\sqrt{{x}−\mathrm{1}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}\:}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\frac{\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left\{\left(\sqrt{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left(\sqrt{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+{c}_{\mathrm{2}} \right. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *