Question Number 130533 by mathmax by abdo last updated on 26/Jan/21
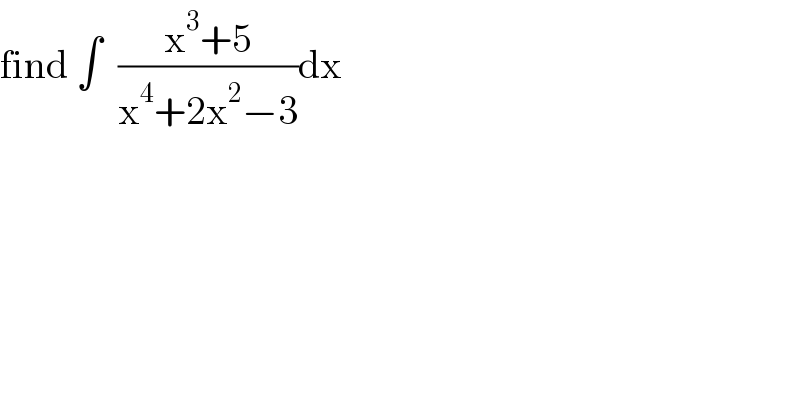
$$\mathrm{find}\:\int\:\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{5}}{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} −\mathrm{3}}\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jan/21
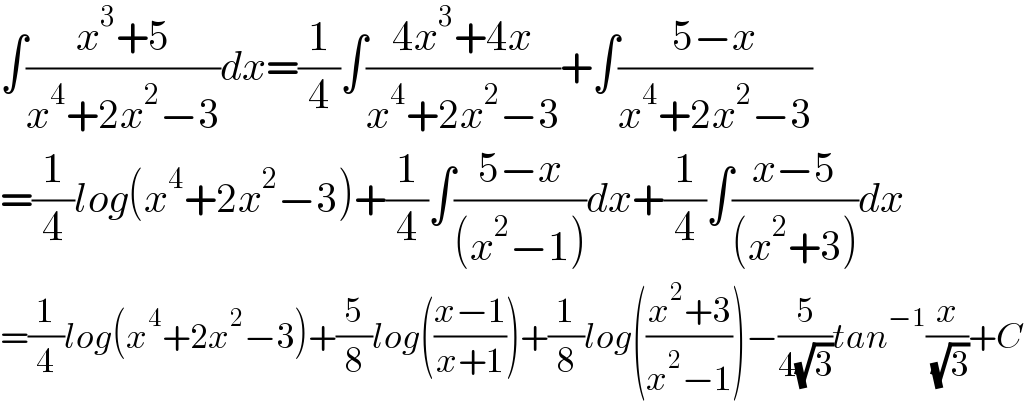
$$\int\frac{{x}^{\mathrm{3}} +\mathrm{5}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4}{x}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}}+\int\frac{\mathrm{5}−{x}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{log}\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{5}−{x}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{dx}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{x}−\mathrm{5}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{log}\left({x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}\right)+\frac{\mathrm{5}}{\mathrm{8}}{log}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{8}}{log}\left(\frac{{x}^{\mathrm{2}} +\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{1}}\right)−\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$
Commented by mathmax by abdo last updated on 27/Jan/21

$$\mathrm{thankx}\:\mathrm{sir} \\ $$
