Menu Close

Find-x-48log-a-4-5log-4-a-a-8-

Tinku Tara 0 Comments
Pin




Question Number 41797 by Tawa1 last updated on 12/Aug/18
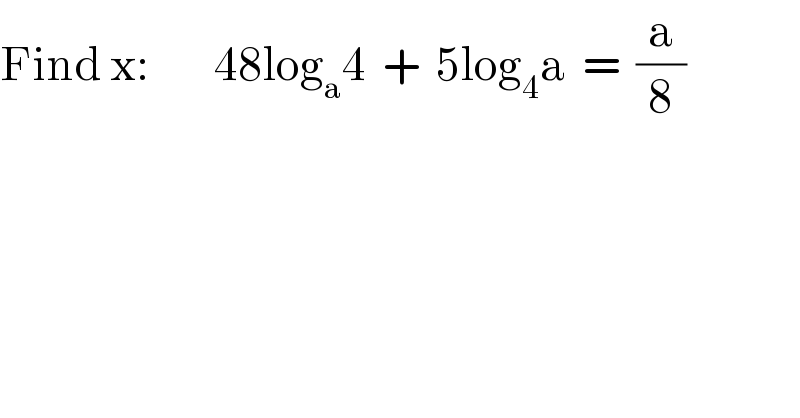
Find x: 48log_a 4 + 5log_4 a = (a/8)
$$\mathrm{Find}\:\mathrm{x}:\:\:\:\:\:\:\:\:\mathrm{48log}_{\mathrm{a}} \mathrm{4}\:\:+\:\:\mathrm{5log}_{\mathrm{4}} \mathrm{a}\:\:=\:\:\frac{\mathrm{a}}{\mathrm{8}} \\ $$
Answered by alex041103 last updated on 13/Aug/18
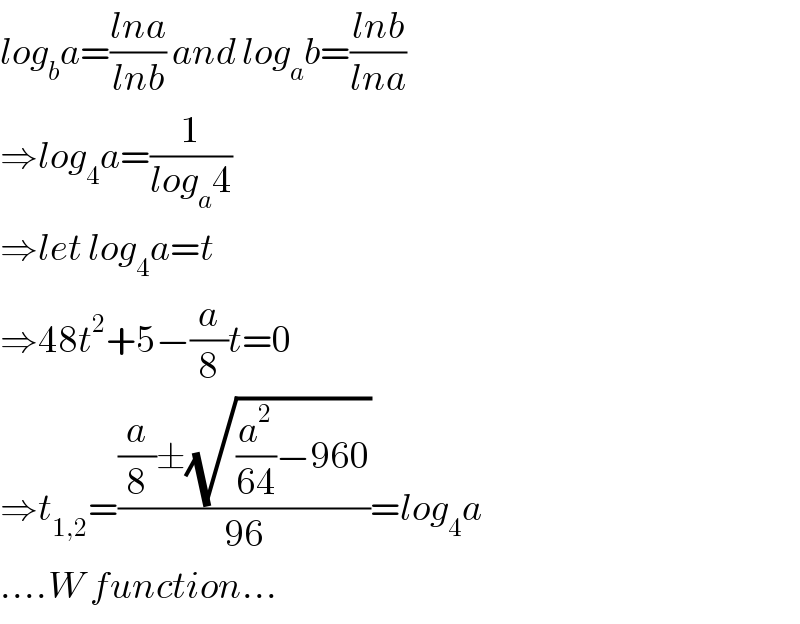
log_b a=((lna)/(lnb)) and log_a b=((lnb)/(lna)) ⇒log_4 a=(1/(log_a 4)) ⇒let log_4 a=t ⇒48t^2 +5−(a/8)t=0 ⇒t_(1,2) =(((a/8)±(√((a^2 /(64))−960)))/(96))=log_4 a ....W function...
$${log}_{{b}} {a}=\frac{{lna}}{{lnb}}\:{and}\:{log}_{{a}} {b}=\frac{{lnb}}{{lna}} \\ $$$$\Rightarrow{log}_{\mathrm{4}} {a}=\frac{\mathrm{1}}{{log}_{{a}} \mathrm{4}} \\ $$$$\Rightarrow{let}\:{log}_{\mathrm{4}} {a}={t} \\ $$$$\Rightarrow\mathrm{48}{t}^{\mathrm{2}} +\mathrm{5}−\frac{{a}}{\mathrm{8}}{t}=\mathrm{0} \\ $$$$\Rightarrow{t}_{\mathrm{1},\mathrm{2}} =\frac{\frac{{a}}{\mathrm{8}}\pm\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{64}}−\mathrm{960}}}{\mathrm{96}}={log}_{\mathrm{4}} {a} \\ $$$$….{W}\:{function}… \\ $$
Commented by Tawa1 last updated on 13/Aug/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MrW3 last updated on 13/Aug/18
working is not correct sir! solution for ax^2 +bx+c=0 is x=((−b±(√(b^2 −4ac)))/(2a)) only when a,b,c are constants, i.e. when they are indepentent from x! but in 48t^2 +5−(a/8)t=0 t and a are dependent from each other, so you may not apply the formula for quadratic equation. if I have an eqn. like this (x^2 −1)^2 +2x(x^2 −1)+1=0 you can not solve it like this: x^2 −1=((−2x±(√(4x^2 −4)))/2)=−x±(√(x^2 −1))
$${working}\:{is}\:{not}\:{correct}\:{sir}! \\ $$$${solution}\:{for} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${is}\:{x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}}\:{only}\: \\ $$$${when}\:{a},{b},{c}\:{are}\:{constants},\:{i}.{e}.\:{when} \\ $$$${they}\:{are}\:{indepentent}\:{from}\:{x}! \\ $$$${but}\:{in}\:\mathrm{48}{t}^{\mathrm{2}} +\mathrm{5}−\frac{{a}}{\mathrm{8}}{t}=\mathrm{0}\:{t}\:{and}\:{a}\:{are}\:{dependent} \\ $$$${from}\:{each}\:{other},\:{so}\:{you}\:{may}\:{not}\:{apply} \\ $$$${the}\:{formula}\:{for}\:{quadratic}\:{equation}. \\ $$$${if}\:{I}\:{have}\:{an}\:{eqn}.\:{like}\:{this} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{x}\left({x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$${you}\:{can}\:{not}\:{solve}\:{it}\:{like}\:{this}: \\ $$$${x}^{\mathrm{2}} −\mathrm{1}=\frac{−\mathrm{2}{x}\pm\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}=−{x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by Tawa1 last updated on 15/Aug/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by alex041103 last updated on 18/Aug/18
That is not a problem.If you have seen the derivation of the quadratic equation, it is made by doing valid algebraic manipulation.In our case, we are in fact just transforming the equation into some other equation, we aren′t solving it. We just use the quadratic equation to transform it into some other equation which is more familiar...
$${That}\:{is}\:{not}\:{a}\:{problem}.{If}\:{you}\:{have}\:{seen} \\ $$$${the}\:{derivation}\:{of}\:{the}\:{quadratic}\:{equation}, \\ $$$${it}\:{is}\:{made}\:{by}\:{doing}\:{valid}\:{algebraic} \\ $$$${manipulation}.{In}\:{our}\:{case},\:{we}\:{are} \\ $$$${in}\:{fact}\:{just}\:{transforming}\:{the}\:{equation} \\ $$$${into}\:{some}\:{other}\:{equation},\:{we}\:{aren}'{t}\:{solving}\:{it}. \\ $$$${We}\:{just}\:{use}\:{the}\:{quadratic}\:{equation} \\ $$$${to}\:{transform}\:{it}\:{into}\:{some}\:{other}\:{equation} \\ $$$${which}\:{is}\:{more}\:{familiar}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *