Menu Close

Find-x-625-x-5-200-x-3-

Tinku Tara 0 Comments
Pin




Question Number 41921 by Tawa1 last updated on 15/Aug/18
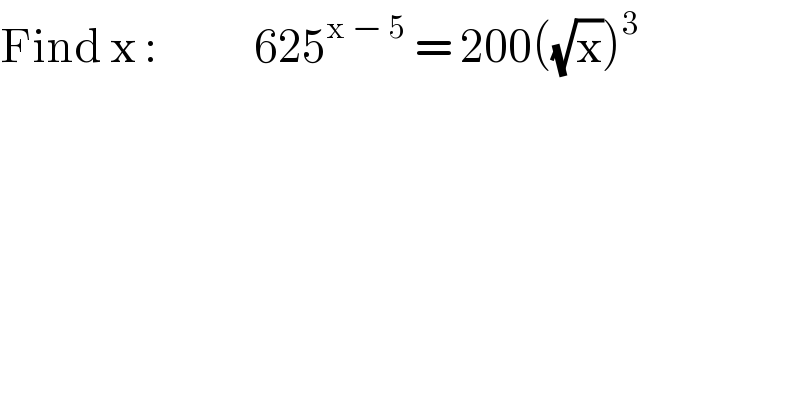
Find x : 625^(x − 5) = 200((√x))^3
$$\mathrm{Find}\:\mathrm{x}\::\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{625}^{\mathrm{x}\:−\:\mathrm{5}} \:=\:\mathrm{200}\left(\sqrt{\mathrm{x}}\right)^{\mathrm{3}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Aug/18
(5^4 )^(x−5) =5^2 ×2^3 ×x^(3/2) 5^(4x−20−2) =2^3 ×x^(3/2) 5^(4x−22) =2^3 ×x^(3/2) (5^(4x−22) /x^(3/2) )=2^3 see left hand side N_r =5^(4x−22) the last digit of its value is either 1 or 5 D_r =x^(2/3) if its value is f(5) then (N_r /D_r )=φ(5) but right hand side 2^3 ...feasibility to bechecked N_r =5^(4x−22) devided by anynumber can not yeild f(2)
$$\left(\mathrm{5}^{\mathrm{4}} \right)^{{x}−\mathrm{5}} =\mathrm{5}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{3}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{5}^{\mathrm{4}{x}−\mathrm{20}−\mathrm{2}} =\mathrm{2}^{\mathrm{3}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{5}^{\mathrm{4}{x}−\mathrm{22}} =\mathrm{2}^{\mathrm{3}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{5}^{\mathrm{4}{x}−\mathrm{22}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }=\mathrm{2}^{\mathrm{3}} \\ $$$${see}\:{left}\:{hand}\:{side}\:{N}_{{r}} =\mathrm{5}^{\mathrm{4}{x}−\mathrm{22}} \:\:{the}\:{last}\:{digit}\:{of} \\ $$$${its}\:{value}\:{is}\:{either}\:\mathrm{1}\:{or}\:\mathrm{5} \\ $$$${D}_{{r}} ={x}^{\frac{\mathrm{2}}{\mathrm{3}}} {if}\:{its}\:{value}\:{is}\:\:{f}\left(\mathrm{5}\right)\:{then} \\ $$$$\frac{{N}_{{r}} }{{D}_{{r}} }=\phi\left(\mathrm{5}\right) \\ $$$${but}\:{right}\:{hand}\:{side}\:\mathrm{2}^{\mathrm{3}} …{feasibility}\:{to}\:{bechecked} \\ $$$${N}_{{r}} =\mathrm{5}^{\mathrm{4}{x}−\mathrm{22}} \:\:{devided}\:{by}\:{anynumber}\:\:{can}\:{not}\:{yeild}\:{f}\left(\mathrm{2}\right) \\ $$
Commented by Tawa1 last updated on 15/Aug/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\: \\ $$
Commented by Tawa1 last updated on 15/Aug/18
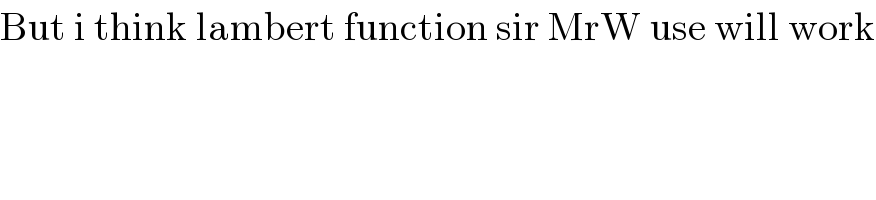
But i think lambert function sir MrW use will work
$$\mathrm{But}\:\mathrm{i}\:\mathrm{think}\:\mathrm{lambert}\:\mathrm{function}\:\mathrm{sir}\:\mathrm{MrW}\:\mathrm{use}\:\mathrm{will}\:\mathrm{work} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Aug/18
i know lambart function but never face the problem in school and college life...so it is bdtter MrW_(3 ) solve it and go through my reasoning
$${i}\:{know}\:{lambart}\:{function}\:{but}\:{never}\:{face}\:{the}\:{problem} \\ $$$${in}\:{school}\:{and}\:{college}\:{life}…{so}\:{it}\:{is}\:{bdtter} \\ $$$${MrW}_{\mathrm{3}\:} \:{solve}\:{it}\:{and}\:{go}\:{through}\:{my}\:{reasoning} \\ $$
Commented by Tawa1 last updated on 17/Aug/18
But you are very good sir. God will help all of you that help us.
$$\mathrm{But}\:\mathrm{you}\:\mathrm{are}\:\mathrm{very}\:\mathrm{good}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{will}\:\mathrm{help}\:\mathrm{all}\:\mathrm{of}\:\mathrm{you}\:\mathrm{that}\:\mathrm{help}\:\mathrm{us}.\: \\ $$
Answered by MrW3 last updated on 17/Aug/18
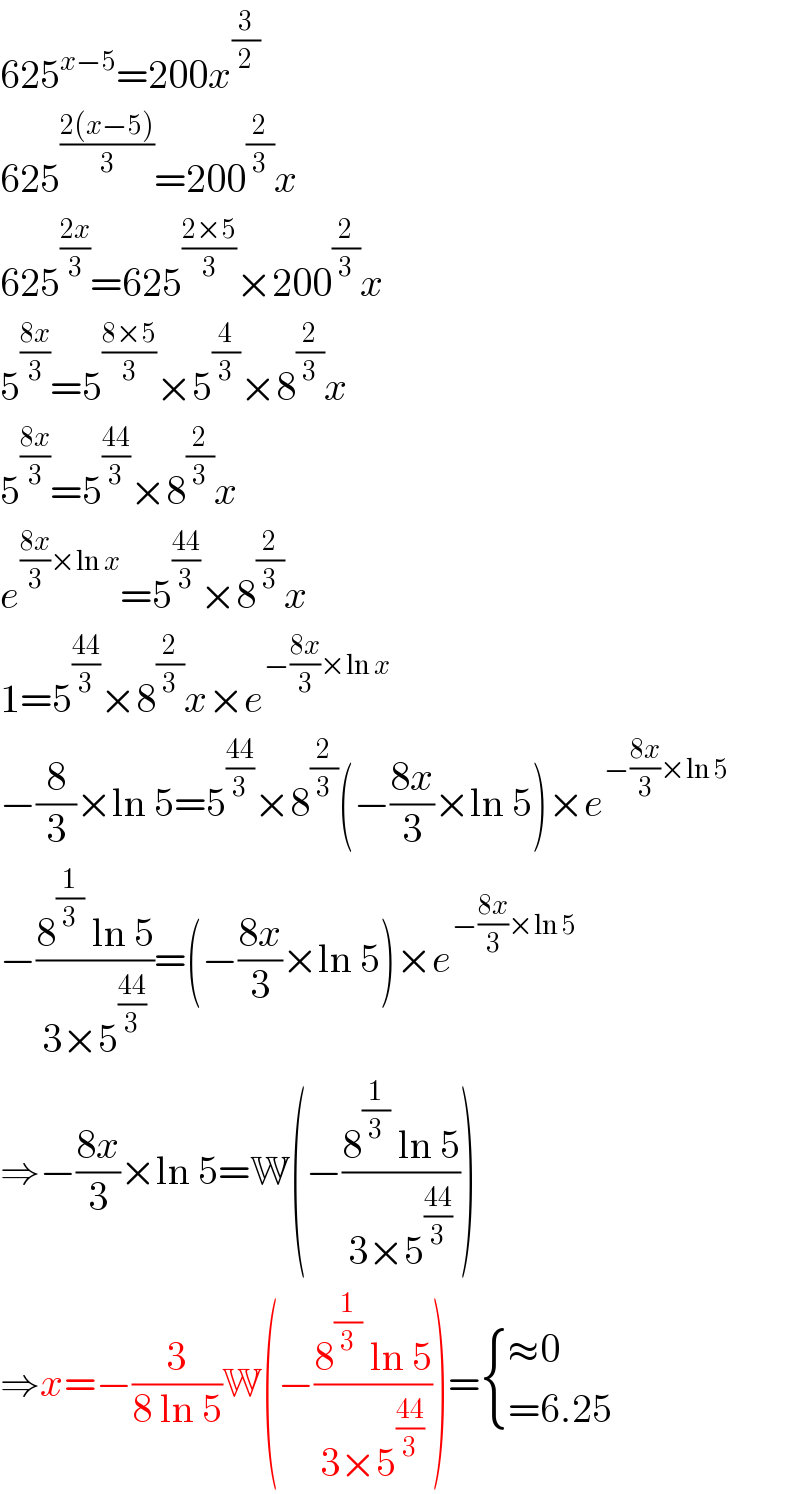
625^(x−5) =200x^(3/2) 625^((2(x−5))/3) =200^(2/3) x 625^((2x)/3) =625^((2×5)/3) ×200^(2/3) x 5^((8x)/3) =5^((8×5)/3) ×5^(4/3) ×8^(2/3) x 5^((8x)/3) =5^((44)/3) ×8^(2/3) x e^(((8x)/3)×ln x) =5^((44)/3) ×8^(2/3) x 1=5^((44)/3) ×8^(2/3) x×e^(−((8x)/3)×ln x) −(8/3)×ln 5=5^((44)/3) ×8^(2/3) (−((8x)/3)×ln 5)×e^(−((8x)/3)×ln 5) −((8^(1/3) ln 5)/(3×5^((44)/3) ))=(−((8x)/3)×ln 5)×e^(−((8x)/3)×ln 5) ⇒−((8x)/3)×ln 5=W(−((8^(1/3) ln 5)/(3×5^((44)/3) ))) ⇒x=−(3/(8 ln 5))W(−((8^(1/3) ln 5)/(3×5^((44)/3) )))= { ((≈0)),((=6.25)) :}
$$\mathrm{625}^{{x}−\mathrm{5}} =\mathrm{200}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{625}^{\frac{\mathrm{2}\left({x}−\mathrm{5}\right)}{\mathrm{3}}} =\mathrm{200}^{\frac{\mathrm{2}}{\mathrm{3}}} {x} \\ $$$$\mathrm{625}^{\frac{\mathrm{2}{x}}{\mathrm{3}}} =\mathrm{625}^{\frac{\mathrm{2}×\mathrm{5}}{\mathrm{3}}} ×\mathrm{200}^{\frac{\mathrm{2}}{\mathrm{3}}} {x} \\ $$$$\mathrm{5}^{\frac{\mathrm{8}{x}}{\mathrm{3}}} =\mathrm{5}^{\frac{\mathrm{8}×\mathrm{5}}{\mathrm{3}}} ×\mathrm{5}^{\frac{\mathrm{4}}{\mathrm{3}}} ×\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} {x} \\ $$$$\mathrm{5}^{\frac{\mathrm{8}{x}}{\mathrm{3}}} =\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} ×\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} {x} \\ $$$${e}^{\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:{x}} =\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} ×\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} {x} \\ $$$$\mathrm{1}=\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} ×\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} {x}×{e}^{−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:{x}} \\ $$$$−\frac{\mathrm{8}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}=\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} ×\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}\right)×{e}^{−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}} \\ $$$$−\frac{\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{ln}\:\mathrm{5}}{\mathrm{3}×\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} }=\left(−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}\right)×{e}^{−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}} \\ $$$$\Rightarrow−\frac{\mathrm{8}{x}}{\mathrm{3}}×\mathrm{ln}\:\mathrm{5}=\mathbb{W}\left(−\frac{\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{ln}\:\mathrm{5}}{\mathrm{3}×\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} }\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{3}}{\mathrm{8}\:\mathrm{ln}\:\mathrm{5}}\mathbb{W}\left(−\frac{\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{ln}\:\mathrm{5}}{\mathrm{3}×\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} }\right)=\begin{cases}{\approx\mathrm{0}}\\{=\mathrm{6}.\mathrm{25}}\end{cases} \\ $$
Commented by Tawa1 last updated on 15/Aug/18
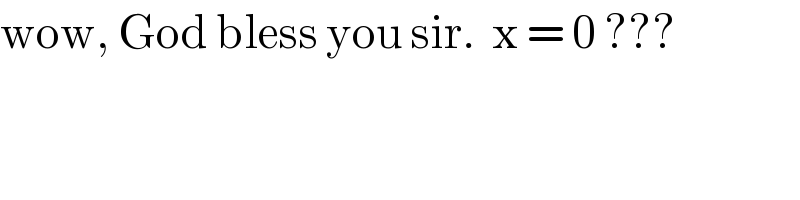
wow, God bless you sir. x = 0 ???
$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{x}\:=\:\mathrm{0}\:??? \\ $$
Commented by MrW3 last updated on 16/Aug/18
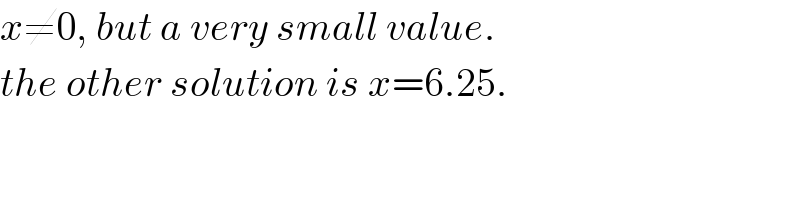
x≠0, but a very small value. the other solution is x=6.25.
$${x}\neq\mathrm{0},\:{but}\:{a}\:{very}\:{small}\:{value}. \\ $$$${the}\:{other}\:{solution}\:{is}\:{x}=\mathrm{6}.\mathrm{25}. \\ $$
Commented by Tawa1 last updated on 16/Aug/18
God bless you sir. i appreciate your effort
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$
Commented by Tawa1 last updated on 16/Aug/18
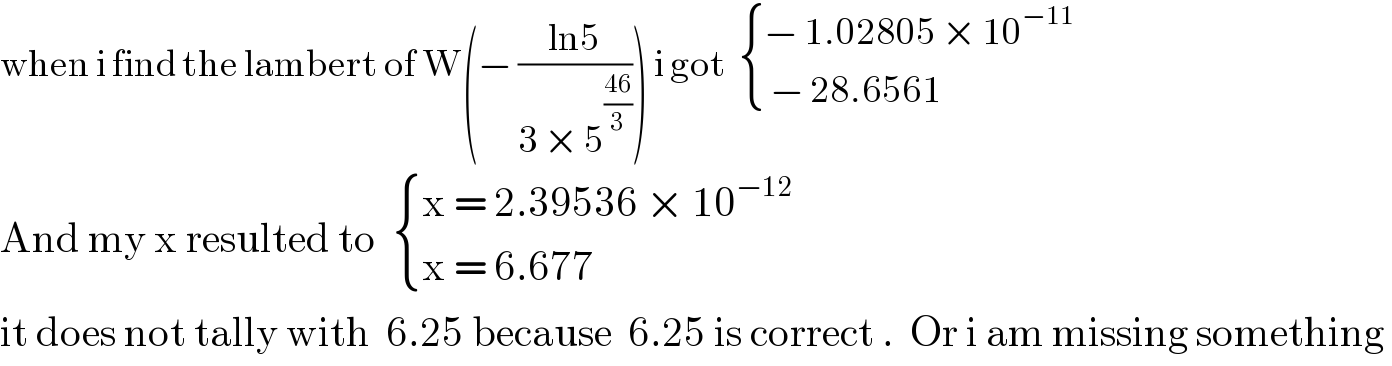
when i find the lambert of W(− ((ln5)/(3 × 5^((46)/3) ))) i got { ((− 1.02805 × 10^(−11) )),(( − 28.6561)) :} And my x resulted to { ((x = 2.39536 × 10^(−12) )),((x = 6.677)) :} it does not tally with 6.25 because 6.25 is correct . Or i am missing something
$$\mathrm{when}\:\mathrm{i}\:\mathrm{find}\:\mathrm{the}\:\mathrm{lambert}\:\mathrm{of}\:\mathrm{W}\left(−\:\frac{\mathrm{ln5}}{\mathrm{3}\:×\:\mathrm{5}^{\frac{\mathrm{46}}{\mathrm{3}}} }\right)\:\mathrm{i}\:\mathrm{got}\:\:\begin{cases}{−\:\mathrm{1}.\mathrm{02805}\:×\:\mathrm{10}^{−\mathrm{11}} }\\{\:−\:\mathrm{28}.\mathrm{6561}}\end{cases} \\ $$$$\mathrm{And}\:\mathrm{my}\:\mathrm{x}\:\mathrm{resulted}\:\mathrm{to}\:\:\begin{cases}{\mathrm{x}\:=\:\mathrm{2}.\mathrm{39536}\:×\:\mathrm{10}^{−\mathrm{12}} }\\{\mathrm{x}\:=\:\mathrm{6}.\mathrm{677}}\end{cases} \\ $$$$\mathrm{it}\:\mathrm{does}\:\mathrm{not}\:\mathrm{tally}\:\mathrm{with}\:\:\mathrm{6}.\mathrm{25}\:\mathrm{because}\:\:\mathrm{6}.\mathrm{25}\:\mathrm{is}\:\mathrm{correct}\:.\:\:\mathrm{Or}\:\mathrm{i}\:\mathrm{am}\:\mathrm{missing}\:\mathrm{something}\: \\ $$
Commented by MrW3 last updated on 17/Aug/18
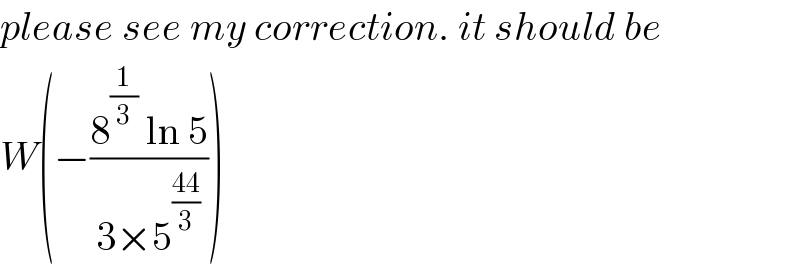
please see my correction. it should be W(−((8^(1/3) ln 5)/(3×5^((44)/3) )))
$${please}\:{see}\:{my}\:{correction}.\:{it}\:{should}\:{be} \\ $$$${W}\left(−\frac{\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{ln}\:\mathrm{5}}{\mathrm{3}×\mathrm{5}^{\frac{\mathrm{44}}{\mathrm{3}}} }\right) \\ $$
Commented by Tawa1 last updated on 17/Aug/18
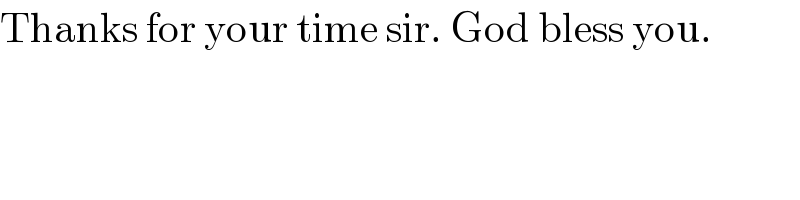
Thanks for your time sir. God bless you.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by Tawa1 last updated on 17/Aug/18
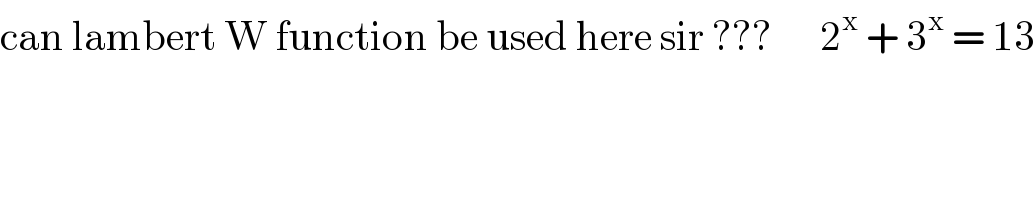
can lambert W function be used here sir ??? 2^x + 3^x = 13
$$\mathrm{can}\:\mathrm{lambert}\:\mathrm{W}\:\mathrm{function}\:\mathrm{be}\:\mathrm{used}\:\mathrm{here}\:\mathrm{sir}\:???\:\:\:\:\:\:\mathrm{2}^{\mathrm{x}} \:+\:\mathrm{3}^{\mathrm{x}} \:=\:\mathrm{13} \\ $$
Commented by Tawa1 last updated on 17/Aug/18
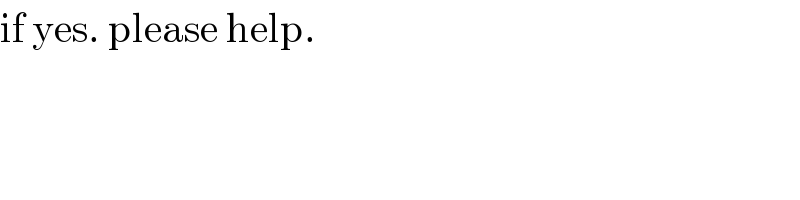
if yes. please help.
$$\mathrm{if}\:\mathrm{yes}.\:\mathrm{please}\:\mathrm{help}. \\ $$
Commented by MrW3 last updated on 17/Aug/18
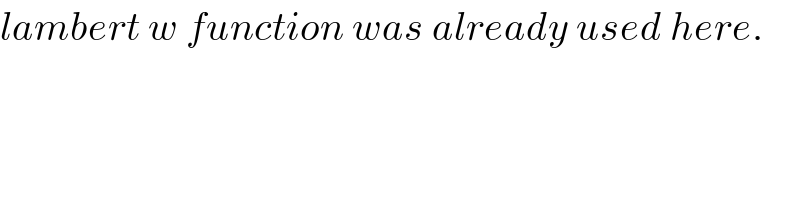
lambert w function was already used here.
$${lambert}\:{w}\:{function}\:{was}\:{already}\:{used}\:{here}. \\ $$
Commented by Tawa1 last updated on 17/Aug/18
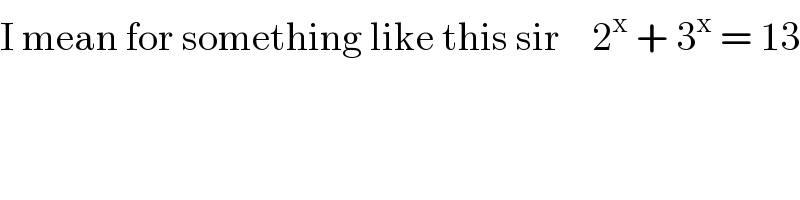
I mean for something like this sir 2^x + 3^x = 13
$$\mathrm{I}\:\mathrm{mean}\:\mathrm{for}\:\mathrm{something}\:\mathrm{like}\:\mathrm{this}\:\mathrm{sir}\:\:\:\:\mathrm{2}^{\mathrm{x}} \:+\:\mathrm{3}^{\mathrm{x}} \:=\:\mathrm{13} \\ $$
Commented by Tawa1 last updated on 17/Aug/18
I learnt how to find the W from you sir. that is why i can complete the solution. Thanks for your help sir. God bless you.
$$\mathrm{I}\:\mathrm{learnt}\:\mathrm{how}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{W}\:\mathrm{from}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{that}\:\mathrm{is}\:\mathrm{why}\:\mathrm{i}\:\mathrm{can}\:\mathrm{complete}\:\mathrm{the} \\ $$$$\mathrm{solution}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by Tawa1 last updated on 17/Aug/18
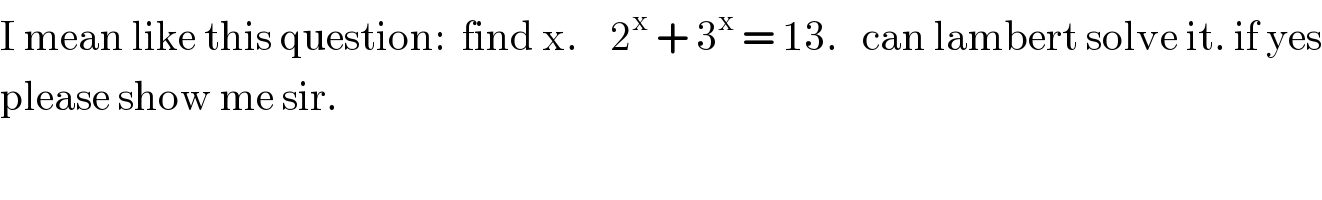
I mean like this question: find x. 2^x + 3^x = 13. can lambert solve it. if yes please show me sir.
$$\mathrm{I}\:\mathrm{mean}\:\mathrm{like}\:\mathrm{this}\:\mathrm{question}:\:\:\mathrm{find}\:\mathrm{x}.\:\:\:\:\mathrm{2}^{\mathrm{x}} \:+\:\mathrm{3}^{\mathrm{x}} \:=\:\mathrm{13}.\:\:\:\mathrm{can}\:\mathrm{lambert}\:\mathrm{solve}\:\mathrm{it}.\:\mathrm{if}\:\mathrm{yes} \\ $$$$\mathrm{please}\:\mathrm{show}\:\mathrm{me}\:\mathrm{sir}. \\ $$
Commented by MrW3 last updated on 17/Aug/18
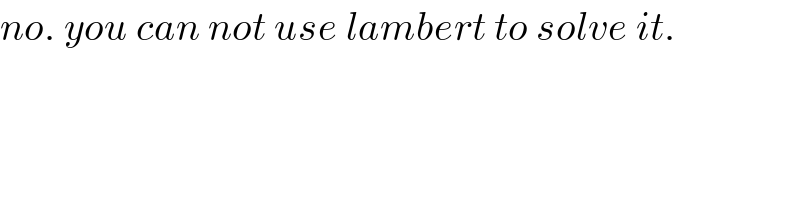
no. you can not use lambert to solve it.
$${no}.\:{you}\:{can}\:{not}\:{use}\:{lambert}\:{to}\:{solve}\:{it}. \\ $$
Commented by Tawa1 last updated on 17/Aug/18
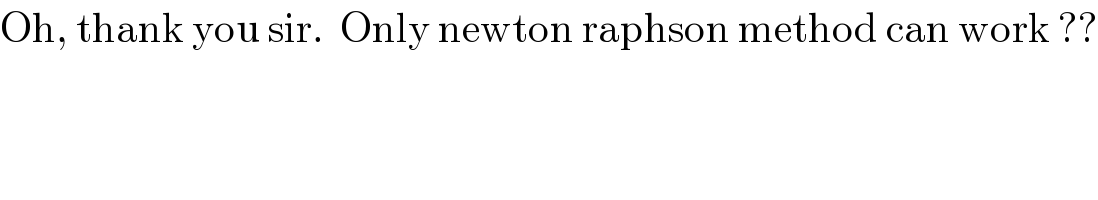
Oh, thank you sir. Only newton raphson method can work ??
$$\mathrm{Oh},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{Only}\:\mathrm{newton}\:\mathrm{raphson}\:\mathrm{method}\:\mathrm{can}\:\mathrm{work}\:?? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *