Question Number 156808 by MathSh last updated on 15/Oct/21

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\int\:\frac{\mathrm{x}^{\mathrm{7}} \:-\:\mathrm{x}^{\mathrm{5}} \:+\:\mathrm{x}^{\mathrm{3}} \:-\:\mathrm{x}}{\mathrm{1}\:+\:\mathrm{x}^{\mathrm{10}} }\:\mathrm{dx}\:\:;\:\:\mathrm{x}\in\mathbb{R} \\ $$
Commented by tabata last updated on 15/Oct/21
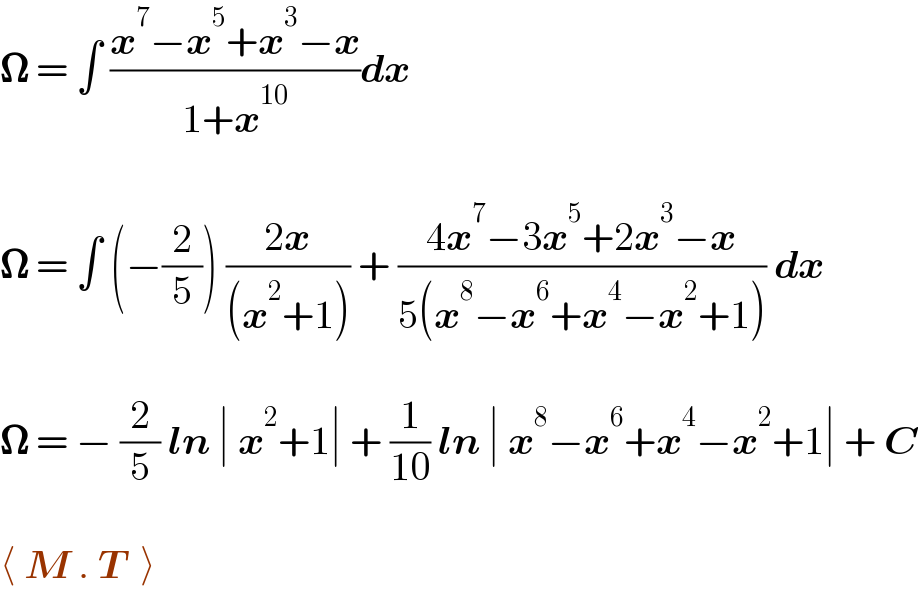
$$\boldsymbol{\Omega}\:=\:\int\:\frac{\boldsymbol{{x}}^{\mathrm{7}} −\boldsymbol{{x}}^{\mathrm{5}} +\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{10}} }\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{\Omega}\:=\:\int\:\left(−\frac{\mathrm{2}}{\mathrm{5}}\right)\:\frac{\mathrm{2}\boldsymbol{{x}}}{\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)}\:+\:\frac{\mathrm{4}\boldsymbol{{x}}^{\mathrm{7}} −\mathrm{3}\boldsymbol{{x}}^{\mathrm{5}} +\mathrm{2}\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}}{\mathrm{5}\left(\boldsymbol{{x}}^{\mathrm{8}} −\boldsymbol{{x}}^{\mathrm{6}} +\boldsymbol{{x}}^{\mathrm{4}} −\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)}\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{\Omega}\:=\:−\:\frac{\mathrm{2}}{\mathrm{5}}\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\mid\:+\:\frac{\mathrm{1}}{\mathrm{10}}\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{x}}^{\mathrm{8}} −\boldsymbol{{x}}^{\mathrm{6}} +\boldsymbol{{x}}^{\mathrm{4}} −\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\mid\:+\:\boldsymbol{{C}} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
